题目内容
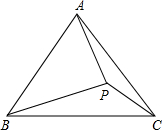
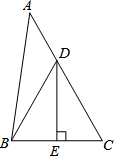
如图,点D是线段AB与线段BC的垂直平分线的交点,∠B=40°,则∠ADC等于( )

| A.50° | B.60° | C.70° | D.80° |

连接BD,AC.设∠1=x,
∵点D是线段AB与线段BC的垂直平分线的交点,
∴AD=BD,BD=CD,
∴∠1=∠2=x,∠4=∠ABD=40°+x,
根据三角形的内角和定理,得∠ADB=180°-2∠4=100°-2x,∠BDC=180°-2x,
∴∠ADC=∠BDC-∠ADB=80°.
故选D.

∵点D是线段AB与线段BC的垂直平分线的交点,
∴AD=BD,BD=CD,
∴∠1=∠2=x,∠4=∠ABD=40°+x,
根据三角形的内角和定理,得∠ADB=180°-2∠4=100°-2x,∠BDC=180°-2x,
∴∠ADC=∠BDC-∠ADB=80°.
故选D.


练习册系列答案
相关题目