题目内容
为了激发学生学习英语的兴趣,萧山区某中学举行了校园英文歌曲大赛,并设立了一、二、三等奖.学校计划根据设奖情况共买50件奖品,其中购买二等奖奖品件数比一等奖奖品件数的2倍还少10件,购买三等奖奖品所花钱数不超过二等奖所花钱数的1.5倍.其中各种奖品的单价如下表所示.如果计划一等奖奖品买x件,买50件奖品的总费用是w元.
(1)用含有x的代数式表示:该校团委购买二等奖奖品多少件,三等奖奖品多少件?并表示w与x的函数关系式;
(2)请问共有几种购买方案?
(3)请你计算一下,学校应如何购买这三种奖品,才能使所支出的总费用最少,最少是多少元?
| 奖品 | 一等奖奖品 | 二等奖奖品 | 三等奖奖品 |
| 单价(元) | 12 | 10 | 5 |
(2)请问共有几种购买方案?
(3)请你计算一下,学校应如何购买这三种奖品,才能使所支出的总费用最少,最少是多少元?
考点:一次函数的应用,一元一次不等式组的应用
专题:
分析:(1)设一等奖奖品买x件,则二等奖奖品件数比一等奖奖品件数的2倍还少10件为(2x-10),进一步表示出三等奖;分别算出三种奖品的费用相加即是总费用;
(2)再根据题意列出不等式组即可求解;
(3)一次函数的系数k=17,故根据函数的性质可知w随x的增大而增大.根据题(1)可求最小值.
(2)再根据题意列出不等式组即可求解;
(3)一次函数的系数k=17,故根据函数的性质可知w随x的增大而增大.根据题(1)可求最小值.
解答:解:(1)购买二等奖为(2x-10)件;
购买三等奖为(60-3x)件.
w=12x+10(2x-10)+5[50-x-(2x-10)]=17x+200;
(2)由题意可得:
,
解得:10≤x<20,
∵x为整数,
∴共有10种方案;
(3)∵k=17>0,
∴w随着x的增大而增大,
∴当x=10时,w有最小值,最小值为w=17×10+200=370(元).
答:当购买一等奖10件,二等奖10件,三等奖30件时所花的费用最少,最少为370元.
购买三等奖为(60-3x)件.
w=12x+10(2x-10)+5[50-x-(2x-10)]=17x+200;
(2)由题意可得:
|
解得:10≤x<20,
∵x为整数,
∴共有10种方案;
(3)∵k=17>0,
∴w随着x的增大而增大,
∴当x=10时,w有最小值,最小值为w=17×10+200=370(元).
答:当购买一等奖10件,二等奖10件,三等奖30件时所花的费用最少,最少为370元.
点评:本题考查一次函数与一元一次不等式组的应用,将现实生活中的事件与数学思想联系起来,读懂题列出不等式关系式即可求解.利用函数的单调性来求最值问题是常用的方法之一,要熟练掌握.

练习册系列答案
相关题目
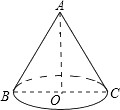 已知圆锥底面半径为4cm,侧面积为32πcm2,设圆锥的母线与高的夹角为θ,如图,则tanθ的值( )
已知圆锥底面半径为4cm,侧面积为32πcm2,设圆锥的母线与高的夹角为θ,如图,则tanθ的值( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
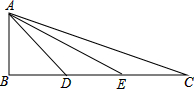 如图,在△ABC,∠B=90°,AB=BD=DE=EC,则下列结论中成立的是( )
如图,在△ABC,∠B=90°,AB=BD=DE=EC,则下列结论中成立的是( )| A、△ACD∽△EAD |
| B、△ABD∽△ABC |
| C、△ABE∽△ABC |
| D、△ABE∽△ACD |
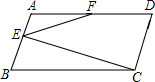 在?ABCD中,BC=2AB,CE⊥AB于E,F为AD中点,∠AEF=50°,求∠A度数.
在?ABCD中,BC=2AB,CE⊥AB于E,F为AD中点,∠AEF=50°,求∠A度数.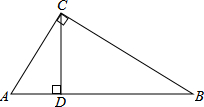 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AD=3,CD=6,求BC的长.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AD=3,CD=6,求BC的长.