题目内容
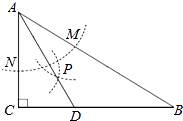
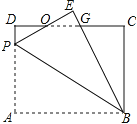
【题目】如图,矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,BE与CD相交于点G,且OE=OD,则AP的长为______.

【答案】4.8.
【解析】解:如图所示:∵四边形ABCD是矩形,
∴∠D=∠A=∠C=90°,AD=BC=6,CD=AB=8,
根据题意得:△ABP≌△EBP,
∴EP=AP,∠E=∠A=90°,BE=AB=8,
在△ODP和△OEG中,
![]() ,
,
∴△ODP≌△OEG(ASA),
∴OP=OG,PD=GE,
∴DG=EP,
设AP=EP=x,则PD=GE=6﹣x,DG=x,
∴CG=8﹣x,BG=8﹣(6﹣x)=2+x,
根据勾股定理得:BC2+CG2=BG2,
即62+(8﹣x)2=(x+2)2,
解得:x=4.8,
∴AP=4.8;
故答案为:4.8.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目