��Ŀ����
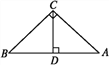
����Ŀ����ͼ����ABC�ǵȱ������Σ�AB=4cm��CD��AB�ڵ�D������P�ӵ�A��������AC��2cm/s���ٶ����յ�C�˶�������P��������P��PQ��BC������AD��DC�ڵ�Q����PQΪ�����ȱ�������PQR�����ı���APRQ���ACD�ص�����ͼ�ε����ΪS��cm2������P�˶���ʱ��Ϊt��s����
��1������Q���߶�AD��ʱ���ú�t�Ĵ���ʽ��ʾQR�ij���
��2�����R�˶���·�̳���
��3������Q���߶�AD��ʱ����S��t֮��ĺ�����ϵʽ��
��4��ֱ��д���Ե�B��Q��RΪ�������������ֱ��������ʱt��ֵ��
���𰸡�
��1��
�⣺��ͼ�٣�
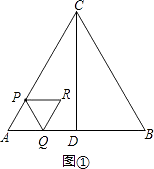
�ߡ�ABC�ǵȱ������Σ�
���ACB=��B=60�㣮
��PQ��BC��
���APQ=��ACB=60�㣬��AQP=��B=60�㣬
���APQ�ǵȱ������Σ�
��PQ=AP=2t��
�ߡ�PQR�ǵȱ������Σ�
��QR=PQ=2t
��2��
�⣺����A��AG��BC�ڵ�G����ͼ�ڣ�
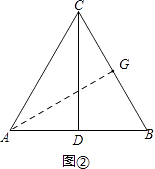
���R�˶���·�̳���AG+CG��
��Rt��AGC�У���AGC=90�㣬sin60��= ![]() =
= ![]() ��cos60��=
��cos60��= ![]() =
= ![]() ��AC=4��
��AC=4��
��AG=2 ![]() ��CG=2��
��CG=2��
���R�˶���·�̳�2 ![]() +2
+2
��3��
�⣺�ٵ�0��t�� ![]() ʱ����ͼ�ۣ�
ʱ����ͼ�ۣ�
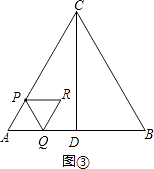
S=S����APRQ=2��S����APQ=2�� ![]() ����2t��2=2
����2t��2=2 ![]() t2��
t2��
�ڵ� ![]() ��t��1ʱ����ͼ��
��t��1ʱ����ͼ��
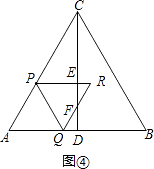
PE=PCsin��PCE=��4��2t���� ![]() =2��t��
=2��t��
��ER=PR��PE=2t����2��t��=3t��2��
��EF=ERtanR= ![]() ��3t��2��
��3t��2��
��S=S����APRQ��S��REF
=2 ![]() t2��
t2�� ![]() ��3t��2��2=��
��3t��2��2=�� ![]() t2+6
t2+6 ![]() t��2
t��2 ![]()
��4��
�⣺t= ![]() ��t=
��t= ![]()
��ʾ���ٵ���QRB=90��ʱ����ͼ�ݣ�

cos��RQB= ![]() =
= ![]() ��
��
��QB=2QR=2QA��
��AB=3QA=6t=4��
��t= ![]() ��
��
�ڵ���RQB=90��ʱ����ͼ�ޣ�
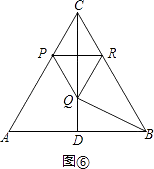
ͬ���ɵ�BC=3RC=3PC=3��4��2t��=4��
��t= ![]()
����������1����֤��APQ�ǵȱ������Σ����ɵõ�QR=PQ=AP=2t����2������A��AG��BC�ڵ�G����ͼ�ڣ��õ�R�˶���·�̳���AG+CG��ֻ�����AG��CG�Ϳɽ�����⣻��3���ı���APRQ���ACD�ص�����ͼ�ο��������Σ�Ҳ����������Σ������������ۣ�Ȼ�����ø���Ϳɽ�����⣻��4������ֱ�Ƕ��㲻ȷ���������������ۣ�ֻ��֡�QRB=90��͡�RQB=90������������ۣ����ɽ�����⣮

����Ŀ�����������ű���2016��3����2016��10��,����բ�ڶ�·����Ϻһ���֡������۴�Ϻ6000���.2017��DZ����Ϻרҵ����С��ץס�̻�,���Լ���ֳ�Ĵ�Ϻ��������.��������ֳ�ɱ��Լ��˷ѵ��������,�����ִ�Ϻ�ijɱ���Ϊ20Ԫ/����.�����г�����,һ�ܵ�������![]() ���������۵���
���������۵���![]() (
(![]() )Ԫ/����Ĺ�ϵ���±�:
)Ԫ/����Ĺ�ϵ���±�:
���۵��� | ... | 30 | 35 | 40 | 45 | ... |
������ | ... | 500 | 450 | 400 | 350 | ... |
(1)ֱ��д��y��x�ĺ�����ϵʽ;
(2)����С��һ�ܵ���������ΪWԪ,�����W��![]() �ĺ�����ϵʽ,��ȷ�������۵�����ʲô��Χ�ڱ仯ʱ,һ�ܵ����������������۵��۵����������?
�ĺ�����ϵʽ,��ȷ�������۵�����ʲô��Χ�ڱ仯ʱ,һ�ܵ����������������۵��۵����������?
(3)������ǮԽ��Խ��,��С������������Ὣһ�ܵ���������ȫ����������и���Ժ.��һ����С�����ܳɱ�������4000Ԫ,�������С������������Ƕ���Ԫ?