题目内容
【题目】如图,已知一个直角三角形纸片ACB,其中∠ACB=90°,AC=4,BC=3,E,F分别是AC,AB边上点,连接EF,将纸片ACB的一角沿EF折叠.
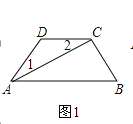
(1)如图①,若折叠后点A落在AB边上的点D处,且使S四边形ECBF=3S△AEF , 则AE=;
(2)如图②,若折叠后点A落在BC边上的点M处,且使MF∥CA.求AE的长;
(3)如图③,若折叠后点A落在BC延长线上的点N处,且使NF⊥AB.求AE的长.
【答案】
(1)![]()
(2)解:设AE=x,则CE=4﹣x.
由折叠可知:AE=EM=x,AF=MF,∠AFE=∠MFE,
∵MF∥AC,
∴∠AEF=∠MFE.
∴∠AEF=∠AFE.
∴AE=AF.
∴AE=EM=MF=AF,
∴四边形AEMF为菱形.
∴EM∥AB.∴△CME∽△CBA.
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,解得x=
,解得x= ![]() ,即AE=
,即AE= ![]()
(3)解:设AE=y,则CE=4﹣y.
由折叠可知:AE=EN=y,AF=NF,
∵NF⊥AB,
∴∠NFB=90°.
∵∠ACB=90°,
∴∠NFB=∠ACB.
且∠NBF=∠ABC,
∴△NBF∽ABC.
∴ ![]() =
= ![]() =
= ![]() .即BF=
.即BF= ![]() NF=
NF= ![]() AF.由BF+AF=AB=5,
AF.由BF+AF=AB=5,
解得:BF= ![]() ,NF=
,NF= ![]() ,
,
∴BN= ![]() =
= ![]() ,
,
∴CN=BN﹣BC= ![]() ﹣3=
﹣3= ![]() .
.
在Rt△CEN中,由勾股定理得:CN2+CE2=EN2,
∴( ![]() )2+(4﹣y)2=y2,
)2+(4﹣y)2=y2,
解得:y= ![]() ,
,
即AE= ![]()
【解析】解:(1)∵△ACB的一角沿EF折叠,折叠后点A落在AB边上的点D处,
∴EF⊥AB,△AEF≌△DEF,
∴S△AEF≌S△DEF,
∵S四边形ECBF=3S△EDF,
∴S△ABC=4S△AEF,
在Rt△ABC中,∵∠ACB=90°,AC=4,BC=3,
∴AB= ![]() =5,
=5,
∵∠EAF=∠BAC,
∴△AEF∽△ABC,
∴ ![]() =(
=( ![]() )2,即(
)2,即( ![]() )2=
)2= ![]() ,
,
∴AE= ![]() ;
;
所以答案是: ![]() ;
;
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对翻折变换(折叠问题)的理解,了解折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.