Question

【题目】求证:有两边和第三边上的中线对应相等的两个三角形相等

Answer 1

【答案】证明见解析.

【解析】

根据题目要求画出图形，如图所示，根据已知条件利用SSS求证△ABE≌△A′B′E′，得出∠BAE=∠B′A′E′，同理可得∠CAD=∠C′A′D′，然后可得∠BAC=∠B′A′C′，再利用SAS即可证明△ABC≌△A′B′C′．

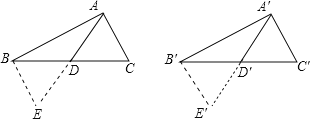
如图所示，在△ABC与△A′B′C′中，AB=A′B′，AC=A′C′，AD和A′D′分别为BC、B′C′

上的中线，且AD=A′D′，

．

求证：△ABC≌△A′B′C′．

证明：∵D、D′分别为BC、B′C′的中点，把△ACD和A′C′D′分别绕D、D′点按顺时针旋转180°可得到△ABE与△A′B′E′，

∴AB=A′B′，BE=B′E′，AE=A′E′，

∴△ABE≌△A′B′E′，

∴∠BAE=∠B′A′E′，

同理可得∠CAD=∠C′A′D′，

∴∠BAC=∠B′A′C′，

∴△ABC≌△A′B′C′．