题目内容
 在直角坐标系中,点P的坐标为(4,3),将OP绕原点逆时针旋转90°得到线段OP′,求P′的坐标和P P′的长度.
在直角坐标系中,点P的坐标为(4,3),将OP绕原点逆时针旋转90°得到线段OP′,求P′的坐标和P P′的长度.
 解:作PA⊥x轴,P'A′⊥x轴,垂足分别为A、A′,
解:作PA⊥x轴,P'A′⊥x轴,垂足分别为A、A′,易证△OPA≌△P'OA',
∴P'A′=OA=4,O'A=AP=3,
∴P'(-3,4),
由勾股定理得PP'=
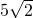 .
.分析:易得OP长.根据旋转角为90°,利用勾股定理可得PP′的长度.过P,P′作出x轴的垂线后,利用AAS可证得OP,OP′所在的直角三角形全等,那么根据第二象限的点的特点可得P′的坐标.
点评:旋转前后对应边相等;利用旋转90°后对应线段所在的直角三角形全等是常用的得到点的坐标的方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
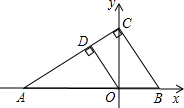 C作CB⊥AC,交x轴于B.
C作CB⊥AC,交x轴于B.