题目内容
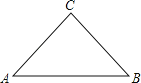
【题目】如图,在等腰直角△ABC中,∠ACB=90°,AC=BC=![]() .
.
(1)作⊙O,使它过点A、B、C(要求:尺规作图,保留作图痕迹,不写作法).
(2)在(1)所作的圆中,圆心角∠BOC= ,圆的半径为 ,劣弧![]() 的长为 .
的长为 .
【答案】(1)画图见解析;(2)90 , 1 , 二分之一π
【解析】(1)作AC、BC的垂直平分线,交于点O,以O为圆心OA长为半径,即可作出;(2)等腰直角△ABC的外接圆的圆心是斜边AB的中点,由等腰三角形底边上的中线、高线和角平分线三线合一,可知CO⊥AB,进而得到∠BOC=90 ,由勾股定理及弧长公式即可求解.
解:(1)⊙O如图所示:

(2)连接CO,
在等腰直角△ABC中,∠ACB=90°,AC=BC=![]()
由勾股定理得:AB=2,
∵∠ACB=90°
∴⊙O的半径=![]() AB=1,
AB=1,
∵O是AB的中点,且AC=BC
∴CO⊥AB
∴∠BOC=90,
∴![]() .
.

练习册系列答案
相关题目