题目内容
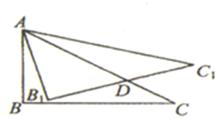
如图,在Rt△ABC中,∠ABC=90°,∠ACB=30°,将△ABC绕点A按逆时针方向旋转15°后得到△AB1C1,B1C1交AC于点D,如果AD=2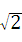 ,则△ABC的周长等于
,则△ABC的周长等于
。
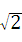 ,则△ABC的周长等于
,则△ABC的周长等于。

3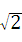 +
+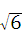 .
.
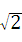 +
+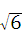 .
.6+2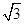 .
.
根据已知可以得出∠BAC=60°,而将△ABC绕点A按逆时针方向旋转15°,可知∠B1AD=45°,可以求出AB1=2,
而AB与AB1是相等的,故可求AB,那么BC和AC可求,则△ABC的周长可求.
解答:解:在Rt△ABC中,∠ABC=90°,∠ACB=30°,
则∠BAC=60°,
将△ABC绕点A按逆时针方向旋转15°后,∠B1AD=45°,
而∠AB1D=90°,故△AB1D是等腰直角三角形,
如果AD=2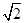 ,则根据勾股定理得,
,则根据勾股定理得,
AB1=2那么AB=AB1=2,
AC=2AB=4,
BC=2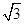 ,
,
△ABC的周长为:AB+BC+AC=2+4+2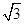 =6+2
=6+2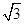 .
.
故本题答案为:6+2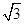 .
.
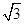 .
.根据已知可以得出∠BAC=60°,而将△ABC绕点A按逆时针方向旋转15°,可知∠B1AD=45°,可以求出AB1=2,
而AB与AB1是相等的,故可求AB,那么BC和AC可求,则△ABC的周长可求.
解答:解:在Rt△ABC中,∠ABC=90°,∠ACB=30°,
则∠BAC=60°,
将△ABC绕点A按逆时针方向旋转15°后,∠B1AD=45°,
而∠AB1D=90°,故△AB1D是等腰直角三角形,
如果AD=2
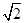 ,则根据勾股定理得,
,则根据勾股定理得,AB1=2那么AB=AB1=2,
AC=2AB=4,
BC=2
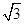 ,
,△ABC的周长为:AB+BC+AC=2+4+2
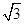 =6+2
=6+2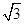 .
.故本题答案为:6+2
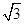 .
.
练习册系列答案
相关题目

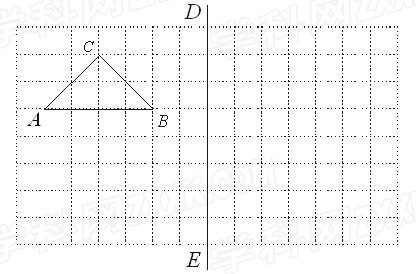
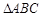 关于直线DE对称的
关于直线DE对称的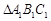 ;
;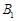 顺时针方向旋转90°后
顺时针方向旋转90°后 的
的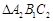 ;
; 在平面直角坐标系中的位置如图所示,其中A(1, 2),B(1, 1),C(3, 1),将△
在平面直角坐标系中的位置如图所示,其中A(1, 2),B(1, 1),C(3, 1),将△ 顺时针旋转
顺时针旋转 后得到△
后得到△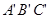 ,则点A旋转到点
,则点A旋转到点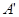 所经过的路线长为
所经过的路线长为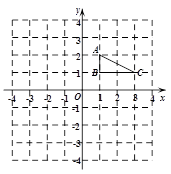
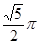
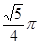

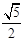


 平行于BC,折叠三角形纸片ABC,使直角顶点B落在直线
平行于BC,折叠三角形纸片ABC,使直角顶点B落在直线