题目内容
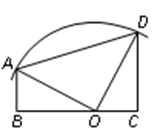
如图,梯形ABCD中,AB∥DC,AB⊥BC,AB=2cm,CD=4cm.以BC上一点O为圆心的圆经过A、D两点,且∠AOD=90°,则圆心O到弦AD的距离是 cm.

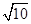 .
.试题分析:易证△AOD是等腰直角三角形.则圆心O到弦AD的距离等于
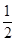 AD,所以可先求AD的长.
AD,所以可先求AD的长.试题解析:以BC上一点O为圆心的圆经过A、D两点,则OA=OD,△AOD是等腰直角三角形.
易证△ABO≌△OCD,则OB=CD=4cm.
在直角△ABO中,根据勾股定理得到OA2=20;
在等腰直角△OAD中,过圆心O作弦AD的垂线OP.
则OP=OA•sin45°=
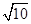 cm.
cm.考点: 1.垂径定理;2.全等三角形的性质;3.勾股定理;4.特殊角的三角函数值.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
 ED,延长DB到点F,使DB到点F,使FB=
ED,延长DB到点F,使DB到点F,使FB=
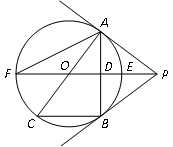
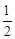 ,求cos∠ACB的值和线段PE的长.
,求cos∠ACB的值和线段PE的长.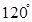 ,半径为
,半径为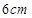 的扇形做成一个圆锥的侧面,这个圆锥的底面的半径是 .
的扇形做成一个圆锥的侧面,这个圆锥的底面的半径是 . 上,且BO=BC,则
上,且BO=BC,则 = .
= .
