题目内容
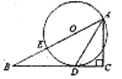
如图,点A,B,C,D在⊙O上,AB=AC,AD与BC相交于点E,AE= ED,延长DB到点F,使DB到点F,使FB=
ED,延长DB到点F,使DB到点F,使FB= BD,连接AF.
BD,连接AF.

⑴△BDE∽△FDA;
⑵试判断直线AF与⊙O的位置关系,并给出证明。
 ED,延长DB到点F,使DB到点F,使FB=
ED,延长DB到点F,使DB到点F,使FB= BD,连接AF.
BD,连接AF.
⑴△BDE∽△FDA;
⑵试判断直线AF与⊙O的位置关系,并给出证明。
(1)证明见解析;(2)相切,证明见解析.
试题分析:(1)因为∠BDE公共,夹此角的两边BD:DF=ED:AD=2:3,由相似三角形的判定,可知△BDE∽△FDA.
(2)连接OA、OB、OC,证明△OAB≌△OAC,得出AO⊥BC.再由△BDE∽△FDA,得出∠EBD=∠AFD,则BE∥FA,从而AO⊥FA,得出直线AF与⊙O相切.
试题解析:(1)在△BDE和△FDA中,
∵FB=
 BD,AE=
BD,AE= ED,AD=AE+ED,FD=FB+BD
ED,AD=AE+ED,FD=FB+BD∴
 ,
,又∵∠BDE=∠FDA,
∴△BDE∽△FDA.
(2)直线AF与⊙O相切.
证明:连接OA,OB,OC,
∵AB=AC,BO=CO,OA=OA,
∴△OAB≌△OAC,
∴∠OAB=∠OAC,
∴AO是等腰三角形ABC顶角∠BAC的平分线,
∴
 ,
,∴AO⊥BC,
∵△BDE∽△FDA,得∠EBD=∠AFD,
∴BE∥FA,
∵AO⊥BE知,AO⊥FA,
∴直线AF与⊙O相切.
考点: 1.切线的判定;2.三角形的角平分线、中线和高;3.相似三角形的判定与性质.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目


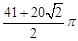 。
。