题目内容
(1)如图,△ABC内接于⊙O,且AB=AC,⊙O的弦AE交于BC于D.求证:AB•AC=AD•AE;
(2)在(1)的条件下当弦AE的延长线与BC的延长线相交于点D时,上述结论是 否还成立?若成立,请给予证明.若不成立,请说明理由.
否还成立?若成立,请给予证明.若不成立,请说明理由.
(1)证明:连接CE,
∵AB=AC,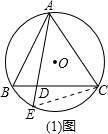
∴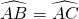 ,
,
∴∠AEC=∠ACD;
又∵∠EAC=∠DAC,
∴△AEC∽△ACD,
∴ ,即AC2=AD•AE;
,即AC2=AD•AE;
又∵AB=AC,
∴AB•AC=AD•AE.
(2)答:上述结论仍成立.
证明:连接BE,
∵AB=AC,
∴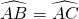 ,
,
∴∠AEB=∠ABD;
又∵∠EAB=∠DAB
∴△AEB∽△ABD,
∴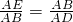 ,即AB2=AD•AE.
,即AB2=AD•AE.
又∵AB=AC,
∴AB•AC=AD•AE.
分析:(1)要证明AB•AC=AD•AE成立,只要能证得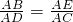 ,要用AB=AC,结合圆,等弧对等角,观察本题无平行关系,首先考虑三角形的相似.连接CE,可证明△AEC∽△ACD,问题解决.
,要用AB=AC,结合圆,等弧对等角,观察本题无平行关系,首先考虑三角形的相似.连接CE,可证明△AEC∽△ACD,问题解决.
(2)假设结论仍成立,考虑作辅助线,看是否有三角形相似,能说明与AB•AC=AD•AE有关的成比例的线段关系.连接BE,可证得△AEB∽△ABD,进而可使问题解决.
点评:有三角形和圆,证明线段成比例关系时,先想到三角形相似,条件不全时,应考虑作辅助线.
∵AB=AC,

∴
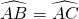 ,
,∴∠AEC=∠ACD;
又∵∠EAC=∠DAC,
∴△AEC∽△ACD,
∴
 ,即AC2=AD•AE;
,即AC2=AD•AE;又∵AB=AC,
∴AB•AC=AD•AE.
(2)答:上述结论仍成立.
证明:连接BE,

∵AB=AC,
∴
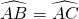 ,
,∴∠AEB=∠ABD;
又∵∠EAB=∠DAB
∴△AEB∽△ABD,
∴
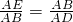 ,即AB2=AD•AE.
,即AB2=AD•AE.又∵AB=AC,
∴AB•AC=AD•AE.
分析:(1)要证明AB•AC=AD•AE成立,只要能证得
 ,要用AB=AC,结合圆,等弧对等角,观察本题无平行关系,首先考虑三角形的相似.连接CE,可证明△AEC∽△ACD,问题解决.
,要用AB=AC,结合圆,等弧对等角,观察本题无平行关系,首先考虑三角形的相似.连接CE,可证明△AEC∽△ACD,问题解决.(2)假设结论仍成立,考虑作辅助线,看是否有三角形相似,能说明与AB•AC=AD•AE有关的成比例的线段关系.连接BE,可证得△AEB∽△ABD,进而可使问题解决.
点评:有三角形和圆,证明线段成比例关系时,先想到三角形相似,条件不全时,应考虑作辅助线.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 如图,△ABC的两个外角的平分线相交于D,若∠B=50°,则∠ADC=( )
如图,△ABC的两个外角的平分线相交于D,若∠B=50°,则∠ADC=( )| A、60° | B、80° | C、65° | D、40° |
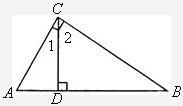
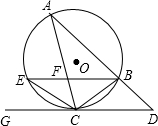 ,且CB=CE.
,且CB=CE.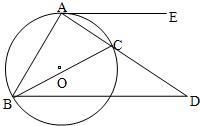 5、已知:如图,△ABC内接于⊙O,AE切⊙O于点A,BD∥AE交AC的延长线于点D,求证:AB2=AC•AD.
5、已知:如图,△ABC内接于⊙O,AE切⊙O于点A,BD∥AE交AC的延长线于点D,求证:AB2=AC•AD.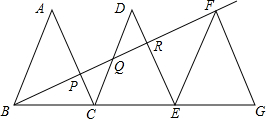 如图,△ABC、△DCE、△FEG是全等的三个等腰三角形,底边BC、CE、EG在同一直线上,且
如图,△ABC、△DCE、△FEG是全等的三个等腰三角形,底边BC、CE、EG在同一直线上,且