题目内容
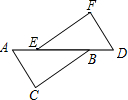 如图,A,E,B,D在同一直线上,在△ABC与△DEF中,AC=DF,AC∥DF.请添加一个条件,然后再正确得出BC=EF.
如图,A,E,B,D在同一直线上,在△ABC与△DEF中,AC=DF,AC∥DF.请添加一个条件,然后再正确得出BC=EF.(1)你添加的条件是
此题答案比唯一,如AB=DE或AE=BD或∠C=∠F或∠ABC=∠DEF或BC∥EF等
此题答案比唯一,如AB=DE或AE=BD或∠C=∠F或∠ABC=∠DEF或BC∥EF等
;(2)写出你的推理过程:
当添加AB=DE时,
∵AC∥DF,
∴∠A=∠D,
在△ABC与△DEF中,
,
∴△ABC≌△DEF(SAS),
∴BC=EF
∵AC∥DF,
∴∠A=∠D,
在△ABC与△DEF中,
|
∴△ABC≌△DEF(SAS),
∴BC=EF
当添加AB=DE时,
∵AC∥DF,
∴∠A=∠D,
在△ABC与△DEF中,
,
∴△ABC≌△DEF(SAS),
∴BC=EF
.∵AC∥DF,
∴∠A=∠D,
在△ABC与△DEF中,
|
∴△ABC≌△DEF(SAS),
∴BC=EF
分析:(1)由全等三角形的判定定理,即可求得答案;
(2)首先由AC∥DF,可得∠A=∠D,又由AC=DF,然后利用全等三角形的判定定理证明即可.
(2)首先由AC∥DF,可得∠A=∠D,又由AC=DF,然后利用全等三角形的判定定理证明即可.
解答:解:(1)添加的条件是:AB=DE或AE=BD或∠C=∠F或∠ABC=∠DEF或BC∥EF等;
(2)∵AC∥DF,
∴∠A=∠D,
①当添加AB=DE时,
在△ABC与△DEF中,
,
∴△ABC≌△DEF(SAS),
∴BC=EF;
②当添加AE=BD时,
∵AE+BE=BD+BE,
即AB=DE,
在△ABC与△DEF中,
,
∴△ABC≌△DEF(SAS),
∴BC=EF;
③当添加∠C=∠F时,
在△ABC与△DEF中,
,
∴△ABC≌△DEF(ASA),
∴BC=EF;
④当添加∠ABC=∠DEF时,
在△ABC与△DEF中,
,
∴△ABC≌△DEF(AAS),
∴BC=EF;
⑤当添加BC∥EF时,
则∠ABC=∠DEF,
在△ABC与△DEF中,
,
∴△ABC≌△DEF(AAS),
∴BC=EF.
故答案为:(1)此题答案比唯一,如AB=DE或AE=BD或∠C=∠F或∠ABC=∠DEF或BC∥EF等;
(2)当添加AB=DE时,
∵AC∥DF,
∴∠A=∠D,
在△ABC与△DEF中,
,
∴△ABC≌△DEF(SAS),
∴BC=EF.
(2)∵AC∥DF,
∴∠A=∠D,
①当添加AB=DE时,
在△ABC与△DEF中,
|
∴△ABC≌△DEF(SAS),
∴BC=EF;
②当添加AE=BD时,
∵AE+BE=BD+BE,
即AB=DE,
在△ABC与△DEF中,
|
∴△ABC≌△DEF(SAS),
∴BC=EF;
③当添加∠C=∠F时,
在△ABC与△DEF中,
|
∴△ABC≌△DEF(ASA),
∴BC=EF;
④当添加∠ABC=∠DEF时,
在△ABC与△DEF中,
|
∴△ABC≌△DEF(AAS),
∴BC=EF;
⑤当添加BC∥EF时,
则∠ABC=∠DEF,
在△ABC与△DEF中,
|
∴△ABC≌△DEF(AAS),
∴BC=EF.
故答案为:(1)此题答案比唯一,如AB=DE或AE=BD或∠C=∠F或∠ABC=∠DEF或BC∥EF等;
(2)当添加AB=DE时,
∵AC∥DF,
∴∠A=∠D,
在△ABC与△DEF中,
|
∴△ABC≌△DEF(SAS),
∴BC=EF.
点评:此题考查了全等三角形的判定与性质以及平行线的性质.此题属于开放题,难度不大,注意掌握全等三角形的判定方法:SSS,SAS,ASA,AAS,HL.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
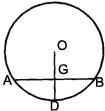 14、如图,已知⊙P的半径OD=5,OD⊥AB,垂足是G,OG=3,则弦AB=
14、如图,已知⊙P的半径OD=5,OD⊥AB,垂足是G,OG=3,则弦AB=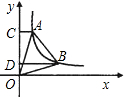 如图,已知A,B两点是反比例函数y=
如图,已知A,B两点是反比例函数y=

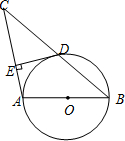 如图AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.
如图AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.