题目内容
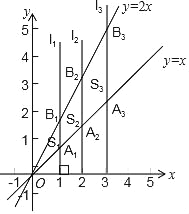
【题目】如图,直线l1⊥x轴于点(1,0),直线l2⊥x轴于点(2,0),直线l3⊥x轴于点(3,0),……直线ln⊥x轴于点(n,0).函数y=x的图象与直线l1、l2、l3、…、ln分别交于点A1、A2、A3、…、An;函数y=2x的图象与直线l1、l2、l3、…、ln分别交于点B1、B2、B3、…、Bn.如果△OA1B1的面积记作S1,四边形A1A2B2B1的面积记作S2,四边形A2A3B3B2的面积记作S3,…,四边形An﹣1AnBnBn﹣1的面积记作Sn,那么S2018=( )
A. 2017.5B. 2018C. 2018.5D. 2019
【答案】A
【解析】
根据直线解析式求出An﹣1Bn﹣1,AnBn的值,再根据直线ln﹣1与直线ln互相平行并判断出四边形An﹣1AnBnBn﹣1是梯形,然后根据梯形的面积公式求出Sn的表达式,然后把n=2013代入表达式进行计算即可得解.
解:根据题意,An﹣1Bn﹣1=2(n﹣1)﹣(n﹣1)=2n﹣2﹣n+1=n﹣1,
AnBn=2n﹣n=n,
∵直线ln﹣1⊥x轴于点(n﹣1,0),直线ln⊥x轴于点(n,0),
∴An﹣1Bn﹣1∥AnBn,且ln﹣1与ln间的距离为1,
∴四边形An﹣1AnBnBn﹣1是梯形,
Sn=![]() (n﹣1+n)×1=
(n﹣1+n)×1=![]() (2n﹣1),
(2n﹣1),
当n=2018时,S2018=![]() (2×2018﹣1)=2017.5.
(2×2018﹣1)=2017.5.
故选:A.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目