题目内容
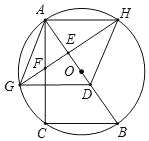
【题目】如图,Rt△ABC,CA⊥BC,AC=4,在AB边上取一点D,使AD=BC,作AD的垂直平分线,交AC边于点F,交以AB为直径的⊙O于G,H,设BC=x.
(1)求证:四边形AGDH为菱形;
(2)若EF=y,求y关于x的函数关系式;
(3)连结OF,CG.
①若△AOF为等腰三角形,求⊙O的面积;
②若BC=3,则![]() CG+9=______.(直接写出答案).
CG+9=______.(直接写出答案).
【答案】(1)证明见解析;(2)y=![]() x2(x>0);(3)①
x2(x>0);(3)①![]() π或8π或(2
π或8π或(2![]() +2)π;②4
+2)π;②4![]() .
.
【解析】
(1)根据线段的垂直平分线的性质以及垂径定理证明AG=DG=DH=AH即可;
(2)只要证明△AEF∽△ACB,可得![]() 解决问题;
解决问题;
(3)①分三种情形分别求解即可解决问题;
②只要证明△CFG∽△HFA,可得![]() =
=![]() ,求出相应的线段即可解决问题;
,求出相应的线段即可解决问题;
(1)证明:∵GH垂直平分线段AD,
∴HA=HD,GA=GD,
∵AB是直径,AB⊥GH,
∴EG=EH,
∴DG=DH,
∴AG=DG=DH=AH,
∴四边形AGDH是菱形.
(2)解:∵AB是直径,
∴∠ACB=90°,
∵AE⊥EF,
∴∠AEF=∠ACB=90°,
∵∠EAF=∠CAB,
∴△AEF∽△ACB,
∴![]() ,
,
∴![]() ,
,
∴y=![]() x2(x>0).
x2(x>0).
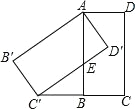
(3)①解:如图1中,连接DF.
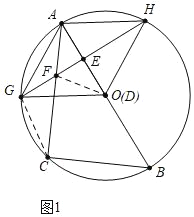
∵GH垂直平分线段AD,
∴FA=FD,
∴当点D与O重合时,△AOF是等腰三角形,此时AB=2BC,∠CAB=30°,
∴AB=![]() ,
,
∴⊙O的面积为![]() π.
π.
如图2中,当AF=AO时,
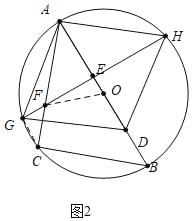
∵AB=![]() =
=![]() ,
,
∴OA=![]() ,
,
∵AF=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得x=4(负根已经舍弃),
∴AB=![]() ,
,
∴⊙O的面积为8π.
如图2﹣1中,当点C与点F重合时,设AE=x,则BC=AD=2x,AB=![]() ,
,
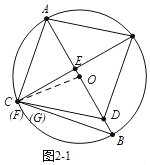
∵△ACE∽△ABC,
∴AC2=AEAB,
∴16=x![]() ,
,
解得x2=2![]() ﹣2(负根已经舍弃),
﹣2(负根已经舍弃),
∴AB2=16+4x2=8![]() +8,
+8,
∴⊙O的面积=π![]() AB2=(2
AB2=(2![]() +2)π
+2)π
综上所述,满足条件的⊙O的面积为![]() π或8π或(2
π或8π或(2![]() +2)π;
+2)π;
②如图3中,连接CG.
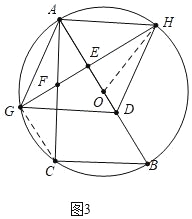
∵AC=4,BC=3,∠ACB=90°,
∴AB=5,
∴OH=OA=![]() ,
,
∴AE=![]() ,
,
∴OE=OA﹣AE=1,
∴EG=EH=![]() =
=![]() ,
,
∵EF=![]() x2=
x2=![]() ,
,
∴FG=![]() ﹣
﹣![]() ,AF=
,AF=![]() =
=![]() ,AH=
,AH=![]() =
=![]() ,
,
∵∠CFG=∠AFH,∠FCG=∠AHF,
∴△CFG∽△HFA,
∴![]() ,
,
∴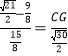 ,
,
∴CG=![]() ﹣
﹣![]() ,
,
∴![]() CG+9=4
CG+9=4![]() .
.
故答案为4![]() .
.

 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案