题目内容
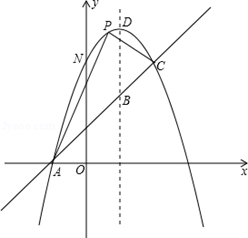
已知:如图一,抛物线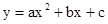 与x轴正半轴交于A、B两点,与y轴交于点C,直线
与x轴正半轴交于A、B两点,与y轴交于点C,直线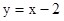 经过A、C两点,且AB=2.
经过A、C两点,且AB=2.

(1)求抛物线的解析式;
(2)若直线DE平行于x轴并从C点开始以每秒1个单位的速度沿y轴正方向平移,且分别交y轴、线段BC于点E,D,同时动点P从点B出发,沿BO方向以每秒2个单位速度运动,(如图2);当点P运动到原点O时,直线DE与点P都停止运动,连DP,若点P运动时间为t秒 ;设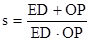 ,当t 为何值时,s有最小值,并求出最小值。
,当t 为何值时,s有最小值,并求出最小值。
(3)在(2)的条件下,是否存在t的值,使以P、B、D为顶点的三角形与△ABC相似;若存在,求t的值;若不存在,请说明理由。
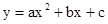 与x轴正半轴交于A、B两点,与y轴交于点C,直线
与x轴正半轴交于A、B两点,与y轴交于点C,直线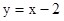 经过A、C两点,且AB=2.
经过A、C两点,且AB=2.
(1)求抛物线的解析式;
(2)若直线DE平行于x轴并从C点开始以每秒1个单位的速度沿y轴正方向平移,且分别交y轴、线段BC于点E,D,同时动点P从点B出发,沿BO方向以每秒2个单位速度运动,(如图2);当点P运动到原点O时,直线DE与点P都停止运动,连DP,若点P运动时间为t秒 ;设
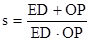 ,当t 为何值时,s有最小值,并求出最小值。
,当t 为何值时,s有最小值,并求出最小值。(3)在(2)的条件下,是否存在t的值,使以P、B、D为顶点的三角形与△ABC相似;若存在,求t的值;若不存在,请说明理由。
(1)y="-1/4" x2+3/2 x-2(2)1(3)当t="2" /3 或t="10/" 7 时,以P、B、D为顶点的三角形与△ABC相似,证明见解析
解:(1)由抛物线y=ax2+bx-2得:C(0,-2),
∴OA=OC=2,
∴A(2,0),
∵△ABC的面积为2,
∴AB=2,
∴B(4,0),
∴设抛物线的解析式为y=a(x-2)(x-4),代入点C(0,-2),
a="-1/4" ,
∴抛物线的解析式为y="-1/4" (x-2)(x-4)="-1/4" x2+3/2 x-2,
答:抛物线的解析式为y="-1/4" x2+3/2 x-2.
(2)解:由题意:CE=t,PB=2t,OP=4-2t,
∵ED∥BA
可得:ED /OB ="CE" /CO ,
即ED/4 ="CE/2" ,
∴ED=2CE=2t,
①1/ED +1/OP ="1/2t" +1/4-2t ="4/2t(4-2t)" ="1/-t2+2t" ,
∵当t=1时,-t2+2t有最大值1,
∴当t=1时1 ED +1 OP 的值最小,最小值为1.
答:当t为1时,1/ED +1/OP 的值最小,最小值是1.
②解:由题意可求:CD=" 5" t,CB="2" 5 ,
∴BD="2" 5 - 5 t,
∵∠PBD=∠ABC,
∴以P、B、D为顶点的三角形与△ABC相似有两种情况:
当BP AB ="BD" BC 时,即2t 2 ="2" 5 - 5 t 2 5 ,
解得:t="2" 3 ,
当BP BD ="BC" BA 时,即2t 2 5 - 5 t ="2" 5 2 ,
解得:t="10" 7 ,
当t="2/3" 或t="10/7" 时,以P、B、D为顶点的三角形与△ABC相似.
答:存在t的值,使以P,B,D为顶点的三角形与△ABC相似,t的值是2/3 或10/7 .
(1)求出C的坐标,得到A、B的坐标,设抛物线的解析式为y=a(x-2)(x-4),代入点C的坐标求出a即可;
(2)①由题意:CE=t,PB=2t,OP=4-2t,由ED∥BA得出EDOB ="CE" CO ,求出ED=2CE=2t,根据1 ED +1 OP ="1" 2t +1 4-2t ="4" 2t(4-2t) ="1" -t2+2t ,求出即可;
②以P、B、D为顶点的三角形与△ABC相似有两种情况:BP AB ="BD" BC 和BP BD ="BC" BA 代入求出即可.
∴OA=OC=2,
∴A(2,0),
∵△ABC的面积为2,
∴AB=2,
∴B(4,0),
∴设抛物线的解析式为y=a(x-2)(x-4),代入点C(0,-2),
a="-1/4" ,
∴抛物线的解析式为y="-1/4" (x-2)(x-4)="-1/4" x2+3/2 x-2,
答:抛物线的解析式为y="-1/4" x2+3/2 x-2.
(2)解:由题意:CE=t,PB=2t,OP=4-2t,
∵ED∥BA
可得:ED /OB ="CE" /CO ,
即ED/4 ="CE/2" ,
∴ED=2CE=2t,
①1/ED +1/OP ="1/2t" +1/4-2t ="4/2t(4-2t)" ="1/-t2+2t" ,
∵当t=1时,-t2+2t有最大值1,
∴当t=1时1 ED +1 OP 的值最小,最小值为1.
答:当t为1时,1/ED +1/OP 的值最小,最小值是1.
②解:由题意可求:CD=" 5" t,CB="2" 5 ,
∴BD="2" 5 - 5 t,
∵∠PBD=∠ABC,
∴以P、B、D为顶点的三角形与△ABC相似有两种情况:
当BP AB ="BD" BC 时,即2t 2 ="2" 5 - 5 t 2 5 ,
解得:t="2" 3 ,
当BP BD ="BC" BA 时,即2t 2 5 - 5 t ="2" 5 2 ,
解得:t="10" 7 ,
当t="2/3" 或t="10/7" 时,以P、B、D为顶点的三角形与△ABC相似.
答:存在t的值,使以P,B,D为顶点的三角形与△ABC相似,t的值是2/3 或10/7 .
(1)求出C的坐标,得到A、B的坐标,设抛物线的解析式为y=a(x-2)(x-4),代入点C的坐标求出a即可;
(2)①由题意:CE=t,PB=2t,OP=4-2t,由ED∥BA得出EDOB ="CE" CO ,求出ED=2CE=2t,根据1 ED +1 OP ="1" 2t +1 4-2t ="4" 2t(4-2t) ="1" -t2+2t ,求出即可;
②以P、B、D为顶点的三角形与△ABC相似有两种情况:BP AB ="BD" BC 和BP BD ="BC" BA 代入求出即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,与
,与 轴交于A、B两点,点
轴交于A、B两点,点 为抛物线的顶点。点P在抛物线的对称轴上,设⊙P的半径为
为抛物线的顶点。点P在抛物线的对称轴上,设⊙P的半径为 ,当⊙P与
,当⊙P与
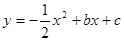 的图象经过A(2,0)B(0,-6)两点
的图象经过A(2,0)B(0,-6)两点
 轴交于点C,连结BA、BC,求△ABC的面积
轴交于点C,连结BA、BC,求△ABC的面积 ,在如图所示的直角坐标系中,求铅球的落点与丁丁的距离.
,在如图所示的直角坐标系中,求铅球的落点与丁丁的距离.
 的图象得到
的图象得到 的图象,则抛物线
的图象,则抛物线
 的顶点坐标是______________.
的顶点坐标是______________.