Question

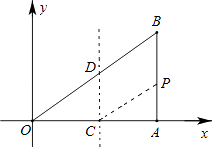
【题目】如图，已知O（0，0）、A（4，0）、B（4，3）．动点P从O点出发，以每秒3个单位的速度，沿△OAB的边OA、AB、BO作匀速运动；动直线l从AB位置出发，以每秒1个单位的速度向x轴负方向作匀速平移运动．若它们同时出发，运动的时间为t秒，当点P运动到O时，它们都停止运动．
（1）当P在线段OA上运动时，求直线l与以P为圆心、1为半径的圆相交时t的取值范围；
（2）当P在线段AB上运动时，设直线l分别与OA、OB交于C、D，试问：四边形CPBD是否可能为菱形？若能，求出此时t的值；若不能，请说明理由，并说明如何改变直线l的出发时间，使得四边形CPBD会是菱形．

Answer 1

【答案】
（1）解：当P在线段OA上运动时，OP=3t，AC=t，

⊙P与直线l相交时， ，

解得 ＜t＜

（2）解：四边形CPBD不可能为菱形．

依题意，得AC=t，OC=4﹣t，PA=3t﹣4，PB=7﹣3t，

∵CD∥AB，

∴ = ，即 = ，

解得CD= （4﹣t），

由菱形的性质，得CD=PB，

即 （4﹣t）=7﹣3t，

解得t= ，

又当四边形CPBD为菱形时，PC=PB=7﹣3t，当t= 时，

代入PA2+AC2=（3t﹣4）2+t2= ，PC2=（7﹣3t）2= ，

∴PA2+AC2≠PC2，就不能构成菱形．

设直线l比P点迟a秒出发，则AC=t﹣a，OC=4﹣t+a，

由CD∥AB，得CD= （4﹣t+a），由CD=PB，得 （4﹣t+a）=7﹣3t，

解得t= ，

PC∥OB，PC=CD，得 = ，即ABPC=OBAP，

3× （4﹣t+a）=5×（3t﹣4），

解得t= ，

则 = ，

解得a= ，即直线l比P点迟 秒出发．

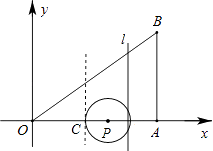
【解析】（1）根据点P与直线l的距离d＜1分为点P在直线l的左边和右边，分别表示距离，列不等式组求范围；（2）四边形CPBD不可能为菱形．依题意可得AC=t，OC=4﹣t，PA=3t﹣4，PB=7﹣3t，由CD∥AB，利用相似比表示CD，由菱形的性质得CD=PB可求t的值，又当四边形CPBD为菱形时，PC=PB=7﹣3t，把t代入PA2+AC2 ， PC2中，看结果是否相等如果结果不相等，就不能构成菱形．设直线l比P点迟a秒出发，则AC=t﹣a，OC=4﹣t+a，再利用平行线表示CD，根据CD=PB，PC∥OB，得相似比，分别表示t，列方程求a即可．
【考点精析】本题主要考查了解一元一次方程的步骤和勾股定理的概念的相关知识点，需要掌握先去分母再括号，移项变号要记牢．同类各项去合并，系数化“1”还没好．求得未知须检验，回代值等才算了；直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题．