��Ŀ����
����Ŀ����֪��A��B�������϶�Ӧ�����ֱ���a��b��ʾ���ң�a��20��2+|b+10|��0��P�������ϵ�һ�����㣮
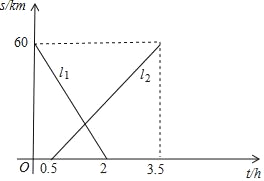
��1���������ϱ��A��B��λ�ã������A��B֮��ľ��룻
��2����֪�߶�OB���е�C��|BC|��6�����������е�P����PB��2PCʱ����P���Ӧ������
��3������P��ԭ�㿪ʼ��һ�������ƶ�1����λ���ȣ��ڶ��������ƶ�3����λ���ȣ������������ƶ�5����λ���ȣ����Ĵ������ƶ�7����λ���ȣ���������P���ƶ�����A��B�غϵ�λ���������ܣ���ֱ�ӻش����ܣ���ֱ��ָ�����ڼ����ƶ�������һ���غϣ�
![]()
���𰸡���1���������������AB��30����2��P���Ӧ����Ϊ��6��2����3����A��ʾ20�����20��P��A�غϣ���B��ʾ��10����P���B���غϣ�
��������
(1)�ȸ��ݷǸ������������a��b��ֵ���������ϱ�ʾ��A��B��λ�ã����������������ľ��빫ʽ�����A��B֮��ľ��뼴�ɣ�
(2)��P���Ӧ����Ϊx����P������PB=2PCʱ��������������ۣ�����PB=2PC���x��ֵ���ɣ�
(3)���ݵ�һ�ε�P��ʾ-1���ڶ��ε�P��ʾ2����P��ʾ��������Ϊ-3��4��-5��6�����ҳ����ɼ��ɵó����ۣ�
�⣺(1)��(a��20)2+|b+10|��0��
��a��20��b����10��
��AB��20��(��10)��30��
�����ϱ��A��B�ã�
![]()
��2����|BC|��6��C���߶�OB�ϣ�
��xC��(��10)��6��
��xC����4��
��PB��2PC��
��P�ڵ�B���ʱPB��PC�����������������
��P���߶�BC��ʱ��
xP��xB��2(xc��xp)��
��xp+10��2(��4��xp)��
��ã�xp����6��
��P�ڵ�C�Ҳ�ʱ��
xp��xB��2(xp��xc)��
xp+10��2xp+8��
xp��2��
��������P���Ӧ����Ϊ��6��2��
(3)��һ�ε�P��ʾ��1���ڶ��ε�P��ʾ2�����Ω�3��4����5��6��
���n��Ϊ(-1)nn��
��A��ʾ20�����20��P��A�غϣ�
��B��ʾ-10����P���B���غϣ�
�ʴ�Ϊ��(1)AB=30����2��-6��2����3�����A�غϣ����B���غϣ�

 ȫ��������ϵ�д�
ȫ��������ϵ�д� һ��һ����ʱ���ϵ�д�
һ��һ����ʱ���ϵ�д�