题目内容
【题目】如图,在ABCD中,∠ABC的平分线交AD于点E,延长BE交CD的延长线于F.
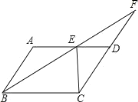
(1)若∠F=40°,求∠A的度数;
(2)若AB=10,BC=16,CE⊥AD,求ABCD的面积.
【答案】(1)100°(2)128
【解析】试题分析:(1)由平行四边形的性质和已知条件得出∠AEB=∠CBF,∠ABE=∠F=40°,证出∠AEB=∠ABE=40°,由三角形内角和定理求出结果即可;(2)由∠AEB=∠ABE得AE=AB=10,由四边形ABCD是平行四边形得AD=BC=16,CD=AB=10,DE=AD﹣AE=6,又CE⊥AD,CE=8,故ABCD的面积=ADCE=128;
试题解析:
(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠AEB=∠CBF,∠ABE=∠F=40°,
∵∠ABC的平分线交AD于点E,
∴∠ABE=∠CBF,
∴∠AEB=∠ABE=40°,
∴∠A=180°﹣40°﹣40°=100°
(2)∵∠AEB=∠ABE
∴AE=AB=10
∵四边形ABCD是平行四边形
∴AD=BC=16,CD=AB=10,
∴DE=AD﹣AE=6,
∵CE⊥AD,
∴CE=8,
∴ABCD的面积=ADCE=16×8=128

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目