题目内容
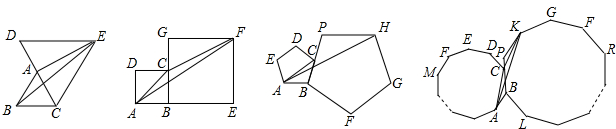
(2012•通州区一模)已知如图,△ABC和△DCE都是等边三角形,若△ABC的边长为1,则△BAE的面积是
.
四边形ABCD和四边形BEFG都是正方形,若正方形ABCD的边长为4,则△FAC的面积是
…
如果两个正多边形ABCDE…和BPKGY…是正n(n≥3)边形,正多边形ABCDE …的边长是2a,则△KCA的面积是
| ||
| 4 |
| ||
| 4 |
四边形ABCD和四边形BEFG都是正方形,若正方形ABCD的边长为4,则△FAC的面积是
8
8
.…
如果两个正多边形ABCDE…和BPKGY…是正n(n≥3)边形,正多边形ABCDE …的边长是2a,则△KCA的面积是
2a2sin
或(4a2•sin
×cos
)
| 360° |
| n |
| 90°(n-2) |
| n |
| 90°(n-2) |
| n |
2a2sin
或(4a2•sin
×cos
)
.(结果用含有a、n的代数式表示)| 360° |
| n |
| 90°(n-2) |
| n |
| 90°(n-2) |
| n |

分析:先根据平行线的判定定理得出AB∥CE,再过点C作CF⊥AB于点F,利用锐角三角函数的定义即可求出CF的长,由三角形的面积公式即可求出△BAE的面积;利用三角形的面积公式即可得出△BAE的面积;连接BF,过点B作BM⊥AC,可先判断出AC∥BF,故可得出BM即为△FAC的高,再根据三角形的面积公式即可得出结论;同以上结论,当两个正多边形ABCDE…和BPKGY…是正n(n≥3)边形,正多边形ABCDE …的边长是2a可得出△ABC与△KCA同底等高,过点B作BN⊥AC于点N,由锐角三角函数的定义可求出BN及AC的长,利用三角形的面积公式即可得出结论.
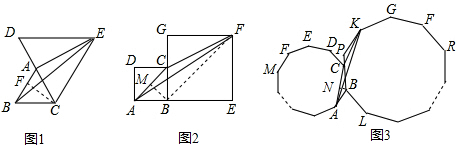
解答:解:如图1,
∵△ABC与△CDE均为等边三角形,
∴∠DCE=∠BAC=60°,
∴AB∥CE,
过点C作CF⊥AB于点F,则CF即为△BAE的高,
∴△ABC与△BAE同底等高,
∴S△BAE=S△ABC=
AB•CF=
×1×
=
;
如图2,连接BF,过点B作BM⊥AC于点M,同理可证AC∥BF,故△FAC与△ABC同底等高,
∴S△FAC=S△ABC=
×4×4=8;
如图3,
正多边形ABCDE…中,过点B作BN⊥AC于点N,同上可得S△KCA=S△ABC,
∵多边形是正多边形,BN⊥AC,
∴∠NBC=
,AC=2NC=2AN,
∵BC=2a,
∴在Rt△BCN中,NC=BC•sin
,BN=BC×cos
,
∴S△KCA=S△ABC=
AC•BN=
×2×2a×sin
×2a×cos
=4a2•sin
×cos
=2a2sin
.
故答案为:2a2sin
或(4a2•sin
×cos
)
∵△ABC与△CDE均为等边三角形,
∴∠DCE=∠BAC=60°,
∴AB∥CE,
过点C作CF⊥AB于点F,则CF即为△BAE的高,
∴△ABC与△BAE同底等高,
∴S△BAE=S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
如图2,连接BF,过点B作BM⊥AC于点M,同理可证AC∥BF,故△FAC与△ABC同底等高,
∴S△FAC=S△ABC=
| 1 |
| 2 |
如图3,
正多边形ABCDE…中,过点B作BN⊥AC于点N,同上可得S△KCA=S△ABC,
∵多边形是正多边形,BN⊥AC,
∴∠NBC=
| 90°×(n-2) |
| n |
∵BC=2a,
∴在Rt△BCN中,NC=BC•sin
| 90°×(n-2) |
| n |
| 90°×(n-2) |
| n |
∴S△KCA=S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 90°×(n-2) |
| n |
| 90°×(n-2) |
| n |
| 90°(n-2) |
| n |
| 90°(n-2) |
| n |
| 360° |
| n |

故答案为:2a2sin
| 360° |
| n |
| 90°(n-2) |
| n |
| 90°(n-2) |
| n |
点评:本题考查的是正多边形和圆,解答此题的关键是根据题意作出辅助线,构造出同底等高的三角形,再根据三角形的面积公式求解.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
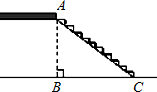 (2012•通州区一模)某地区准备修建一座高AB=6m的过街天桥,已知天桥的坡面AC与地面BC的夹角∠ACB的余弦值为
(2012•通州区一模)某地区准备修建一座高AB=6m的过街天桥,已知天桥的坡面AC与地面BC的夹角∠ACB的余弦值为 (2012•通州区一模)已知四边形ABCD,点E是射线BC上的一个动点(点E不与B、C两点重合),线段BE的垂直平分线交射线AC于点P,连接DP,PE.
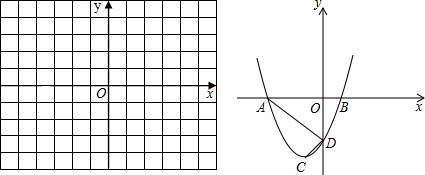
(2012•通州区一模)已知四边形ABCD,点E是射线BC上的一个动点(点E不与B、C两点重合),线段BE的垂直平分线交射线AC于点P,连接DP,PE.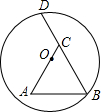 (2012•通州区一模)如图,BD是⊙O的弦,点C在BD上,以BC为边作等边三角形△ABC,点A在圆内,且AC恰好经过点O,其中BC=12,OA=8,则BD的长为( )
(2012•通州区一模)如图,BD是⊙O的弦,点C在BD上,以BC为边作等边三角形△ABC,点A在圆内,且AC恰好经过点O,其中BC=12,OA=8,则BD的长为( )