题目内容
 已知△ABC中,∠ABC与∠ACB的平分线相交于O点
已知△ABC中,∠ABC与∠ACB的平分线相交于O点(1)若∠1+∠2=50°,则∠O=
130°
130°
;(2)若∠ABC+∠ACB=120°,则∠O=
120°
120°
;(3)若∠A=70°,则∠O=
125°
125°
;(4)通过计算,你发现∠O与∠A的关系是什么?并说明理由.
分析:(1)利用三角形内角和定理得出即可;
(2)利用角平分线的性质以及三角形内角和定理得出即可;
(3)利用角平分线的性质以及三角形内角和定理得出即可;
(4)利用角平分线的性质以及三角形内角和定理得出∠O与∠A的关系即可.
(2)利用角平分线的性质以及三角形内角和定理得出即可;
(3)利用角平分线的性质以及三角形内角和定理得出即可;
(4)利用角平分线的性质以及三角形内角和定理得出∠O与∠A的关系即可.
解答:解:(1)∵∠1+∠2=50°,
∴∠O=180°-50°=130°;
故答案为:130°;
(2)∵∠ABC与∠ACB的平分线相交于O点,
∴∠1=
∠ABC,∠2=
∠ACB,
∵∠ABC+∠ACB=120°,
∴∠1+∠2=60°,
∴∠O=180°-60°=120°;
故答案为:120°;
(3)∵∠A=70°,
∴∠ABC+∠ACB=180°-70°=110°,
∵∠ABC与∠ACB的平分线相交于O点,
∴∠1=
∠ABC,∠2=
∠ACB,
∴∠1+∠2=55°,
∴∠O=180°-55°=125°;
故答案为:125°;
(4)∠O=90°+
∠A;
理由:∠O=180°-(∠1+∠2)
=180°-
(∠ABC+∠ACB)
=180°-
(180°-∠A)
=90°+
∠A.
∴∠O=180°-50°=130°;
故答案为:130°;
(2)∵∠ABC与∠ACB的平分线相交于O点,
∴∠1=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠ABC+∠ACB=120°,
∴∠1+∠2=60°,
∴∠O=180°-60°=120°;
故答案为:120°;
(3)∵∠A=70°,
∴∠ABC+∠ACB=180°-70°=110°,
∵∠ABC与∠ACB的平分线相交于O点,
∴∠1=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠1+∠2=55°,
∴∠O=180°-55°=125°;
故答案为:125°;
(4)∠O=90°+
| 1 |
| 2 |
理由:∠O=180°-(∠1+∠2)
=180°-
| 1 |
| 2 |
=180°-
| 1 |
| 2 |
=90°+
| 1 |
| 2 |
点评:此题主要考查了角平分线的性质以及三角形内角和定理等知识,熟练利用角平分线的性质得出是解题关键.

练习册系列答案
 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
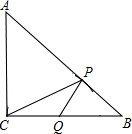 情况;若不可能,请说明理由.
情况;若不可能,请说明理由.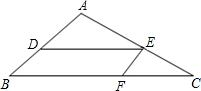 已知△ABC中,DE∥BC,EF∥AB,AB=3,BC=6,AD:DB=2:1,则四边形DBFE的周长为
已知△ABC中,DE∥BC,EF∥AB,AB=3,BC=6,AD:DB=2:1,则四边形DBFE的周长为 如图所示,已知△ABC中,AB=AC,以AB为直径作⊙O交BC于D,交AC于E,过D作DF⊥AC于F
如图所示,已知△ABC中,AB=AC,以AB为直径作⊙O交BC于D,交AC于E,过D作DF⊥AC于F 如图,已知△ABC中,AB=AC,AB垂直平分线交AC于D,连接BE,若∠A=40°,则∠EBC=( )
如图,已知△ABC中,AB=AC,AB垂直平分线交AC于D,连接BE,若∠A=40°,则∠EBC=( )