题目内容
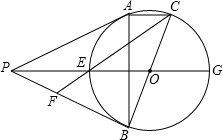 如图,PA、PB是⊙0的切线,切点分别为A、B,BC是⊙0的直径,PO交⊙0于E、G两点,CE交PB于F,连AB,下列结论:①AE=CG ②AC∥PG ③PF=EF ④E为△ABP的内心,其中正确的是( )
如图,PA、PB是⊙0的切线,切点分别为A、B,BC是⊙0的直径,PO交⊙0于E、G两点,CE交PB于F,连AB,下列结论:①AE=CG ②AC∥PG ③PF=EF ④E为△ABP的内心,其中正确的是( )分析:先判断出AB⊥AC且AB⊥PG,继而可得出AC∥PG,判断出②正确;根据AH=HC,可判断出EN=MG,从而可求出AE=CG,判断出①正确;利用切线的性质判断出∠PAE=∠EAB,从而得出点E是△PAB的角平分线的交点,判断出④正确;
解答: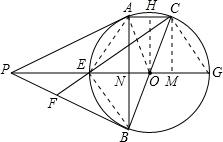
解:连接AE、CG、OA、OC,作OH⊥AC,CM⊥PG,
∵BC是直径,
∴∠BAC=90°,即AB⊥AC,
∵PA、PB是⊙0的切线,
∴PG⊥AB,
故可得AC∥PG,即可得②正确;
∵OA=OC,
∴点H是线段AC的中点,
由题意得,AN=CM,EN=OE-ON,MG=OG-OM,
∴EN=MG,
∴AE=
,CG=
,AE=CG,
即①正确;
由题意得,∠FPE=∠ABC,∠FEP=∠CEO=∠ECO,
而
≠
,故不能得出∠FPE=∠FEP,
也即得出PF≠EF,即③错误;
∵PA、PB是⊙0的切线,
∴∠PAE=∠AEB,
又∵
=
,
∴∠EAB=∠ABE,
∴∠PAE=∠EAB,即可得点E是△PAB角平分线的交点,点E为△ABP的内心,
故可得④正确.
综上可得①②④正确.
故选C.

解:连接AE、CG、OA、OC,作OH⊥AC,CM⊥PG,
∵BC是直径,
∴∠BAC=90°,即AB⊥AC,
∵PA、PB是⊙0的切线,
∴PG⊥AB,
故可得AC∥PG,即可得②正确;
∵OA=OC,
∴点H是线段AC的中点,
由题意得,AN=CM,EN=OE-ON,MG=OG-OM,
∴EN=MG,
∴AE=
| AN2+EN2 |
| CM2+MG2 |
即①正确;
由题意得,∠FPE=∠ABC,∠FEP=∠CEO=∠ECO,
而
 |
| EB |
 |
| AC |
也即得出PF≠EF,即③错误;
∵PA、PB是⊙0的切线,
∴∠PAE=∠AEB,
又∵
 |
| AE |
 |
| EB |
∴∠EAB=∠ABE,
∴∠PAE=∠EAB,即可得点E是△PAB角平分线的交点,点E为△ABP的内心,
故可得④正确.
综上可得①②④正确.
故选C.
点评:此题属于圆的综合题,涉及了圆周角定理、切线的性质及勾股定理的知识,解答本题的关键是熟练掌握切线的几个性质及圆周角定理,难度较大,注意各个知识点之间的融会贯通.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,PA,PB是⊙O的切线,切点分别为A,B,且∠APB=50°,点C是优弧
如图,PA,PB是⊙O的切线,切点分别为A,B,且∠APB=50°,点C是优弧 如图,PA、PB是⊙O的切线,A、B为切点,∠OAB=30度.
如图,PA、PB是⊙O的切线,A、B为切点,∠OAB=30度. 4、如图,PA、PB是⊙O的两条切线,A、B是切点,连接AB,直线PO交AB于M.请你根据圆的对称性,写出△PAB的三个正确的结论.
4、如图,PA、PB是⊙O的两条切线,A、B是切点,连接AB,直线PO交AB于M.请你根据圆的对称性,写出△PAB的三个正确的结论.
 (2012•谷城县模拟)如图,PA、PB是⊙O 的切线,切点分别是A、B,点C是⊙O上异与点A、B的点,如果∠P=60°,那么∠ACB等于
(2012•谷城县模拟)如图,PA、PB是⊙O 的切线,切点分别是A、B,点C是⊙O上异与点A、B的点,如果∠P=60°,那么∠ACB等于