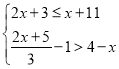题目内容
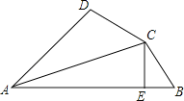
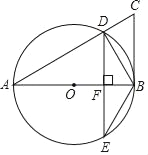
【题目】已知,如图,BC是以线段AB为直径的⊙O的切线,AC交⊙O于点D,过点D作弦DE⊥AB,垂足为点F,连接BD、BE.
(1)仔细观察图形并写出三个不同类型的正确结论:
① ,② ,③ ,(不添加其它字母和辅助线,不必证明);
(2)若∠A=30°,CD=2,求⊙O的半径r.
【答案】(1)结论:DF=FE,BD=BE,△BDF≌△BEF,∠A=∠E等;(2)![]()
【解析】
(1)结论可以有:①DF=FE,BD=BE,②△BDF≌△BEF,③∠A=∠E,∠BDF=∠BEF④BC⊥AB,AD⊥BD,DE∥BC等;由BC是 O的切线,DF⊥AB,得∠AFD=∠CBA=90°;根据DE∥BC和垂径定理知,弧BD=弧BE,DF=FE,BD=BE,由等边对等角得∠E=∠EDB;再由圆周角定理得∠A=∠E,可证△BDF≌△BEF,△BDF∽△BAD;等.
(2)当∠A=30°时,BD=![]() AB=r,∠C=60°,再根据Rt△BCD中,tan60°可求得r=2
AB=r,∠C=60°,再根据Rt△BCD中,tan60°可求得r=2![]() .
.
解:(1)结论:DF=FE,BD=BE,△BDF≌△BEF,∠A=∠E等;
理由:∵AB是直径,DE⊥AB,
∴DF=EF,弧BD=弧BE,
∴BD=BE,
∴Rt△BDF≌Rt△BEF(HL),
根据圆周角定理可知:∠A=∠E.
故答案为DF=EF,BD=BE,Rt△BDF≌Rt△BEF;
(2)∵AB是⊙O的直径,
∴∠ADB=90°,
又∵∠A=30°,
∴BD=ABsinA=ABsin30°=![]() AB=r;
AB=r;
又∵BC是⊙O的切线,
∴∠CBA=90°,
∴∠C=60°;
在Rt△BCD中,
CD=2,
∴![]() =tan60°,
=tan60°,
∴r=2![]() .
.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目