题目内容
【题目】【问题原型】如图1,在四边形ABCD中,∠ADC=90°,AB=AC.点E、F分别为AC、BC的中点,连结EF,DE.试说明:DE=EF.
【探究】如图2,在问题原型的条件下,当AC平分∠BAD,∠DEF=90°时,求∠BAD的大小.
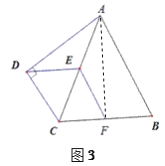
【应用】如图3,在问题原型的条件下,当AB=2,且四边形CDEF是菱形时,直接写出四边形ABCD的面积.

【答案】 【问题原型】详见解析;【探究】∠BAD=60°;【应用】![]()
【解析】试题分析:【问题原型】由三角形中位线定理和直角三角形斜边上的中线等于斜边的一半即可证明 .
【探究】先证明∠EDA=∠DAE=∠CAB=∠CEF,由外角的性质得到∠DEC=2∠DAC=2∠CEF,再由∠DEF=90°,得到∠CEF的度数,即可得到结论.
【应用】连接AF.证明△ECF是等边三角形,从而得到AD,AF的长,由S四边形ABCD=S△ADC+S△ABC=计算即可.
试题解析:解:【问题原型】
证明:在△ABC中,点E,F分别为AC,BC的中点,∴EF∥AB,且EF=![]() AB .
AB .
在Rt△ACD中,点E为AC的中点,∴DE=![]() AC.∵AB=AC,∴DE=EF .
AC.∵AB=AC,∴DE=EF .
【探究】
∵AC平分∠BAD,EF∥AB,DE=![]() AC=AE=EC ,∴∠BAC=∠DAC,∠CEF=∠BAC,
AC=AE=EC ,∴∠BAC=∠DAC,∠CEF=∠BAC,
∠DEC=2∠DAC=∠BAD.∵∠DEF=90°,∴∠CEF+∠DEC=∠BAC+2∠DAC=90°,∴∠BAC=∠DAC=30°,∴∠BAD=60° .
【应用】
连接AF.∵AC=AB,F为BC的中点,∴AF⊥BC.∵四边形CDEF是菱形,∴CF=EF=DE=DC.∵DE=EC=EF=1,∴EC=EF=CF=1,∴△ECF是等边三角形,∴∠ECF=60°,∴∠DCE=60°,∴∠DAC=30°,∴AD=![]() DC=
DC=![]() ,AF=
,AF=![]() CF=
CF=![]() .∴S四边形ABCD=S△ADC+S△ABC=
.∴S四边形ABCD=S△ADC+S△ABC=![]() ADDC+
ADDC+![]() CBAF=
CBAF=![]() =
=![]() .
.

【题目】某校为更好的开展“春季趣味运动会”活动,随机在各年级抽查了部分学生,了解他们最喜爱的趣味运动项目类型(跳绳、实心球、50m、拔河共四类),并将统计结果绘制成如下不完整的频数分布表(如图所示)
根据以上信息回答下列问题:
最喜爱的趣味运动项目类型频数分布表:
项目类型 | 频数 | 频率 |
跳绳 | 25 | a |
实心球 | 20 |
|
50m | b | 0.4 |
拔河 | 0.15 |
(1)直接写出a= ,b= ;
(2)将图中的扇形统计图补充完整(注明项目、百分比);
(3)若全校共有学生1200名,估计该校最喜爱50m和拔河的学生共约有多少人?

【题目】从2012年7月1日起某市执行新版居民阶梯电价,小明同学家收到了新政后的第一张电费单,小明爸爸说:“小明,请你计算一下,这个月的电费支出与新政前相比是多了还是少了?”于是小明上网了解了有关电费的收费情况,得到如下两表:
2004年1月至2012年6月执行的收费标准:
月用电量(度)50度有以下部分 | 50度有以下部分 | 超过50度但不超过200度部分 | 超过200度以上部分 |
单价(元/度) | 0.53 | 0.56 | 0.63 |
2012年7月起执行的收费标准:
月用电量(度) | 230度有以下部分 | 超过230度但不超过400度部分 | 超过400度以上部分 |
单价(元/度) | 0.53 | 0.58 | 0.83 |
(1)若小明家2012年7月份的用电量为200度,则小明家7月份的电费支出是多少元?比新政前少了多少元?
(2)若新政后小明家的月用电量为a度,请你用含a的代数式表示当月的电费支出.



