题目内容
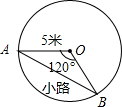 校园内有一个半径为5米的圆形草坪,一部分学生为走“捷径”,在草坪内走出了一条小路AB(如图).通过计算可知,这些学生仅仅少走了
校园内有一个半径为5米的圆形草坪,一部分学生为走“捷径”,在草坪内走出了一条小路AB(如图).通过计算可知,这些学生仅仅少走了分析:首先根据弧长公式求出弧AB的长,进而作AB的弦心距,根据勾股定理和垂径定理求出AB的长,进而可求出少走的步数.
解答: 解:过O作OC⊥AB于C;
解:过O作OC⊥AB于C;
Rt△OAC中,OA=5米,∠AOC=60°;
∴AC=
米,AB=5
米;
又
的长=
=
米;
所以这些学生少走了(
-5
)≈2米;
故只少走了四步.
 解:过O作OC⊥AB于C;
解:过O作OC⊥AB于C;Rt△OAC中,OA=5米,∠AOC=60°;
∴AC=
5
| ||
| 2 |
| 3 |
又
 |
| AB |
| 120×5×π |
| 180 |
| 10π |
| 3 |
所以这些学生少走了(
| 10π |
| 3 |
| 3 |
故只少走了四步.
点评:此题主要考查了垂径定理、勾股定理以及弧长的计算公式.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 如图,校园内有一个半径为12m的圆形草坪,一部分学生为了走“捷径”,走出了一条小路AB.通过计算可知,这些学生仅仅少走了
如图,校园内有一个半径为12m的圆形草坪,一部分学生为了走“捷径”,走出了一条小路AB.通过计算可知,这些学生仅仅少走了| 2 |
| 3 |
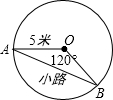 校园内有一个半径为5米的圆形草坪,一部分学生为走“捷径”,在草坪内走出了一条小路AB,如图所示.通过计算可知,这些学生仅仅少走了( )步,却踩坏了花草.(假设2步为1米,结果保留整数)( )
校园内有一个半径为5米的圆形草坪,一部分学生为走“捷径”,在草坪内走出了一条小路AB,如图所示.通过计算可知,这些学生仅仅少走了( )步,却踩坏了花草.(假设2步为1米,结果保留整数)( ) 如图,校园内有一个半径为6m的圆形草坪,一部分学生为了走“捷径”,走出了一条小路AB.通过计算可知,这些学生仅仅少走了
如图,校园内有一个半径为6m的圆形草坪,一部分学生为了走“捷径”,走出了一条小路AB.通过计算可知,这些学生仅仅少走了