题目内容
【题目】（10分）国庆期间，为了满足百姓的消费需求，某商店计划用170000元购进一批家电，这批家电的进价和售价如表：
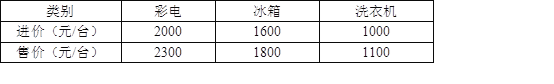
若在现有资金允许的范围内，购买表中三类家电共100台，其中彩电台数是冰箱台数的2倍，设该商店购买冰箱x台．
（1）商店至多可以购买冰箱多少台？
（2）购买冰箱多少台时，能使商店销售完这批家电后获得的利润最大？最大利润为多少元？
【答案】（1）26；（2）购买冰箱26台时，能使商店销售完这批家电后获得的利润最大，最大利润为23000元．
【解析】试题分析：（1）根据三种家电的总进价小于等于170000元列出关于x的不等式，由x为正整数，即可得到答案；
（2）设商店销售完这批家电后获得的利润为y元，则y=500x+10000，结合（1）中x的取值范围，利用一次函数的性质即可解答．
试题解析：（1）根据题意，得：20002x+1600x+1000（100﹣3x）≤170000，解得： 
，∵x为正整数，∴x至多为26．
答：商店至多可以购买冰箱26台．
（2）设商店销售完这批家电后获得的利润为y元，则y=（2300﹣2000）2x+（1800﹣1600）x+（1100﹣1000）（100﹣3x）=500x+10000，∵k=500＞0，∴y随x的增大而增大，∵
且x为正整数，∴当x=26时，y有最大值，最大值为：500×26+10000=23000，
答：购买冰箱26台时，能使商店销售完这批家电后获得的利润最大，最大利润为23000元．
【题目】某自行车厂一周计划生产1400辆自行车，平均每天生产200辆，由于各种原因实际每天生产量与计划量相比有出入
表是某周的生产情况
超产为正、减产为负
：
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 |
|
|
|
|
|
|
|
根据记录可知前三天共生产多少辆；
产量最多的一天比产量最少的一天多生产多少辆；
该厂实行每周计件工资制，每生产一辆车可得60元，若超额完成任务，则超过部分每辆另奖15元；少生产一辆扣15元，那么该厂工人这一周的工资总额是多少？
