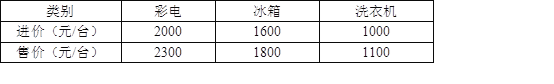��Ŀ����
����Ŀ����ͼ��AB��CD������E��F�ֱ���ֱ��AB��CD�ϣ���ƽ����AB��CD֮����һ����P������0��<��EPF<180��.



��1�����ʡ�AEP����EPF����PFC����������������ϵ��
�⣺���ڵ�P��ƽ����AB��CD֮����һ���㣬�����Ҫ�Ե�P��λ�ý��з������ۣ���ͼ1����P����EF�����ʱ����AEP����EPF����PFC����������ϵΪ______________����ͼ2����P����EF���Ҳ�ʱ����AEP����EPF����PFC����������ϵΪ______________��
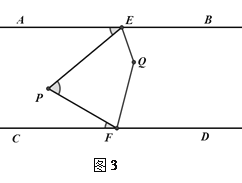
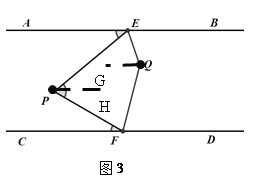
��2����ͼ3��QE��QF�ֱ�ƽ�֡�PEB�͡�PFD���ҵ�P��EF���.
������EPF=60�㣬���EQF=_______��.
�ڲ����EPF���EQF��������ϵ����˵������.
����ͼ4������BEQ���DFQ�Ľ�ƽ���߽��ڵ�Q1����BEQ1���DFQ1�Ľ�ƽ���߽��ڵ�Q2����BEQ2���DFQ2�Ľ�ƽ���߽��ڵ�Q3���˴����ƣ����EPF���EQ2018F����������������ϵ����ֱ��д�������
���𰸡���1����AEP+��PFC=��EPF����AEP+��PFC+��EPF=360�㣻
��2����150��
�ڡ�EPF���EQF��������ϵΪ��EPF+2��EQF=360�㣬�������������
�ۡ�EPF+22019��EQ2018F=360��.
��������
��1����ͼ1������P��PH��AB��֤�� AB��PH��CD��Ȼ�����ƽ���ߵ�����֤�ý��ۣ���ͼ2������P��PH��AB��֤��AB��PH��CD ��Ȼ�����ƽ���ߵ�����֤�ý��ۣ�
��2������ͼ3������P��PH��AB������Q��QG��AB��Ȼ�����ƽ���ߵ����ʵõ���EPF=��AEP+��CFP����EQF=��BEQ+��DFQ ���ɡ�EPF=60�㣬QE��QF�ֱ�ƽ�֡�PEB�͡�PFD��������ý��ۣ�
��ͬ�ټ��ɵý��ۣ�
���ɣ�2����֪��EPF+2��EQF=360�㣬������EPF+22��EQ1F=360�㣬
��EPF+23��EQ2F=360�����ɹ��ɼ�����ý���.
��1����ͼ1������P��PH��AB��
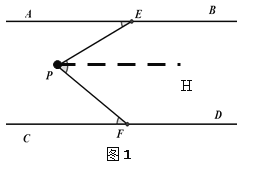
��AB��CD��PH��AB����AB��PH��CD��
���AEP=��EPH����PFC=��FPH��
�ߡ�EPF=��EPH+��FPH��
���EPF=��AEP+��PFC��
��ͼ2������P��PH��AB��
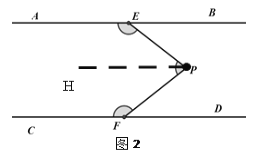
��AB��CD��PH��AB��
��AB��PH��CD��
���AEP+��EPH=180�㣬��CFP+��FPH=180�㣬
�ߡ�EPF=��EPH+��FPH��
���AEP+��PFC+��EPF=360��.
�ʴ�Ϊ��AEP+��PFC=��EPF����AEP+��PFC+��EPF=360�㣻
��2������ͼ3������P��PH��AB������Q��QG��AB��
��AB��CD��PH��AB��
��AB��PH��CD��
���AEP=��EPH����PFC=��FPH��
�ߡ�EPF=��EPH+��FPH��
���EPF=��AEP+��PFC��
ͬ������EQF=��BEQ+��DFQ��
�ߡ�EPF=60�㣬
���AEP+��PFC=60�㣬
���BEP+��DEP=300�㣬
��QE��QF�ֱ�ƽ����PEB����PFD��
���BEQ+��DFQ=150��,
���EQF=150�㣻
��2���ڡ�EPF����EQF��������ϵΪ��EPF+2��EQF=360�㣬
���ɣ�
����1������2������֪��EPF+��BEP+��DFP=360�㣬��EQF=��BEQ+��DFQ��
��QE��QF�ֱ�ƽ����PEB����PFD��
���BEP=2��BEQ����DFP=2��DFQ��
���BEP+��DFP=2����BEQ+��DFQ��=2��EQF��
���EPF+2��EQF=360�㣻
��3���ɣ�2����֪��EPF+2��EQF=360�㣬
ͬ����֤����EPF+22��EQ1F=360�㣬
��EPF+23��EQ2F=360�㣬
����
��EPF+22019��EQ2018F=360�㣬
�ʴ�Ϊ��EPF+22019��EQ2018F=360��.

 һŵ��ҵ�����ҵ���ּ�����������������ϵ�д�
һŵ��ҵ�����ҵ���ּ�����������������ϵ�д�