题目内容
【题目】探索规律:观察下面由“※”组成的图案和算式,解答问题:
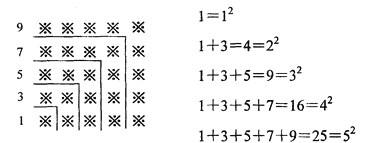
(1)请猜想1+3+5+7+9+…+19=_______________________;
(2)请猜想1+3+5+7+9+…+(2n-1)+(2n+1) =___________;
(3)请用上述规律计算:51+53+55+…+2011+2013.
【答案】(1)100;(2)![]() ;(3)1013424;
;(3)1013424;
【解析】
(1)根据已知得出连续奇数的和等于数字个数的平方;
(2)根据已知得出连续奇数的和等于数字个数的平方,得出答案即可;
(3)用从1开始到2013的和减去从1开始到50的和,然后列式进行计算即可得解.
解:(1)∵1=12,
1+3=4=22,
1+3+5=9=32,
1+3+5+7=16=42,
1+3+5+7+9=25=52,
∴1+3+5+7+9+…+19=102=100;
故答案为:100;
(2)则1+3+5+7+9+…+(2n-1)+(2n+1)=(n+1)2=n2+2n+1;
故答案为:n2+2n+1;
(3)51+53+55+…+2011+2013,
=(![]() )-(
)-(![]() )2,
)2,
=10072-252,
=1014049-626,
=1013424.

练习册系列答案
相关题目