题目内容
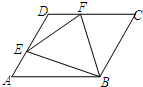 已知:如图,边长为a的菱形ABCD中,∠DAB=60°,E是异于A、D两点的动点,F是CD上的动点,请你判断:无论E、F怎样移动,当满足:AE+CF=a时,△BEF是什么三角形?并说明你的结论.
已知:如图,边长为a的菱形ABCD中,∠DAB=60°,E是异于A、D两点的动点,F是CD上的动点,请你判断:无论E、F怎样移动,当满足:AE+CF=a时,△BEF是什么三角形?并说明你的结论.
 解:△BEF是等边三角形.
解:△BEF是等边三角形.证明:连接BD,
∵菱形ABCD中,∠DAB=60°,
∴△ABD和△BCD是等边三角形,
∴∠BDF=∠A=60°,AB=DB,
∵AE+CF=a,DF+CF=CD=a,
∴AE=DF,
在△ABE和△DBF中,
 ,
,∴△ABE≌△DBF(SAS),
∴∠ABE=∠DBF,BE=BF,
∴∠EBF=∠EBD+∠DBF=∠EBD+∠ABE=∠ABD=60°,
∴△BEF是等边三角形.
分析:首先连接BD,由边长为a的菱形ABCD中,∠DAB=60°,可得△ABD和△BCD是等边三角形,又由AE+CF=a,易证得△ABE≌△DBF,则可得BE=BF,∠EBF=60°,即可证得结论.
点评:此题考查了菱形的性质、等边三角形的判定与性质以及全等三角形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
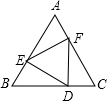 已知:如图,边长为a的正△ABC内有一边长为b的内接正△DEF,则△AEF的内切圆半径为
已知:如图,边长为a的正△ABC内有一边长为b的内接正△DEF,则△AEF的内切圆半径为
 已知:如图,边长为2的圆内接正方形ABCD中,P为边CD的中点,直线AP交圆于E点.求弦DE的长及△PDE的面积.
已知:如图,边长为2的圆内接正方形ABCD中,P为边CD的中点,直线AP交圆于E点.求弦DE的长及△PDE的面积. (1997•南京)已知:如图,边长为2的等边三角形ABC,延长BC到D,使CD=BC,延长CB到E,使BE=CB,求△ADE的周长.
(1997•南京)已知:如图,边长为2的等边三角形ABC,延长BC到D,使CD=BC,延长CB到E,使BE=CB,求△ADE的周长.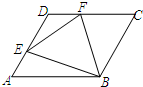 已知:如图,边长为a的菱形ABCD中,∠DAB=60°,E是异于A、D两点的动点,F是CD上的动点,请你判断:无论E、F怎样移动,当满足:AE+CF=a时,△BEF是什么三角形?并说明你的结论.
已知:如图,边长为a的菱形ABCD中,∠DAB=60°,E是异于A、D两点的动点,F是CD上的动点,请你判断:无论E、F怎样移动,当满足:AE+CF=a时,△BEF是什么三角形?并说明你的结论.