题目内容
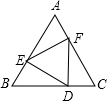 已知:如图,边长为a的正△ABC内有一边长为b的内接正△DEF,则△AEF的内切圆半径为
已知:如图,边长为a的正△ABC内有一边长为b的内接正△DEF,则△AEF的内切圆半径为分析:欲求△AEF的内切圆半径,可以画出图形,然后利用题中已知条件,挖掘隐含条件求解.
解答: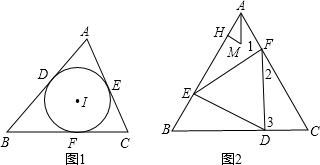 解:如图(1),⊙I是△ABC的内切圆,由切线长定理可得:AD=AE,BD=BF,CE=CF,
解:如图(1),⊙I是△ABC的内切圆,由切线长定理可得:AD=AE,BD=BF,CE=CF,
AD=AE=
[(AB+AC)-(BD+CE)]=
[(AB+AC)-(BF+CF)]=
(AB+AC-BC).
在图(2)中,由于△ABC,△DEF都为正三角形,
∴AB=BC=CA,EF=FD=DE,∠BAC=∠B=∠C=∠FED=∠EFD=∠EDF=60°,
∴∠1+∠2=∠2+∠3=120°,∠1=∠3;
∴△AEF≌△CFD;
同理可证:△AEF≌△CFD≌△BDE;
∴BE=AF,即AE+AF=AE+BE=a.
设M是△AEF的内心,MH⊥AE于H,
则AH=
(AE+AF-EF)=
(a-b);
∵MA平分∠BAC,
∴∠HAM=30°;
∴HM=AH•tan30°=
(a-b)•
=
(a-b).
 解:如图(1),⊙I是△ABC的内切圆,由切线长定理可得:AD=AE,BD=BF,CE=CF,
解:如图(1),⊙I是△ABC的内切圆,由切线长定理可得:AD=AE,BD=BF,CE=CF,AD=AE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
在图(2)中,由于△ABC,△DEF都为正三角形,
∴AB=BC=CA,EF=FD=DE,∠BAC=∠B=∠C=∠FED=∠EFD=∠EDF=60°,
∴∠1+∠2=∠2+∠3=120°,∠1=∠3;
∴△AEF≌△CFD;
同理可证:△AEF≌△CFD≌△BDE;
∴BE=AF,即AE+AF=AE+BE=a.
设M是△AEF的内心,MH⊥AE于H,
则AH=
| 1 |
| 2 |
| 1 |
| 2 |
∵MA平分∠BAC,
∴∠HAM=30°;
∴HM=AH•tan30°=
| 1 |
| 2 |
| ||
| 3 |
| ||
| 6 |
点评:本题考查圆的切线长定理的应用,题目来源于课本例题.

练习册系列答案
相关题目

 已知:如图,边长为2的圆内接正方形ABCD中,P为边CD的中点,直线AP交圆于E点.求弦DE的长及△PDE的面积.
已知:如图,边长为2的圆内接正方形ABCD中,P为边CD的中点,直线AP交圆于E点.求弦DE的长及△PDE的面积. (1997•南京)已知:如图,边长为2的等边三角形ABC,延长BC到D,使CD=BC,延长CB到E,使BE=CB,求△ADE的周长.
(1997•南京)已知:如图,边长为2的等边三角形ABC,延长BC到D,使CD=BC,延长CB到E,使BE=CB,求△ADE的周长.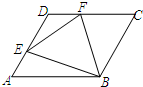 已知:如图,边长为a的菱形ABCD中,∠DAB=60°,E是异于A、D两点的动点,F是CD上的动点,请你判断:无论E、F怎样移动,当满足:AE+CF=a时,△BEF是什么三角形?并说明你的结论.
已知:如图,边长为a的菱形ABCD中,∠DAB=60°,E是异于A、D两点的动点,F是CD上的动点,请你判断:无论E、F怎样移动,当满足:AE+CF=a时,△BEF是什么三角形?并说明你的结论.