题目内容
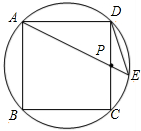 已知:如图,边长为2的圆内接正方形ABCD中,P为边CD的中点,直线AP交圆于E点.求弦DE的长及△PDE的面积.
已知:如图,边长为2的圆内接正方形ABCD中,P为边CD的中点,直线AP交圆于E点.求弦DE的长及△PDE的面积.
分析:连接CE,作出EF⊥CD,运用相似三角形的性质,得出EF,PF的长,即可求出.
解答: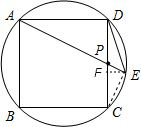 解:连接CE,作EF⊥PF
解:连接CE,作EF⊥PF
∵∠DAP=∠PCE,∠APD=∠CPE,
∴△APD∽△CPE,
∴
=
,
∵P为边CD的中点
∴
=
,
∴PE=
,
∵FE∥AD
∴△APD∽△EPF,
∴
=
,
∴
=
,
∴PF=
,
∴EF=
,
DE=
=
,
△PDE的面积为
×
×1=
.
 解:连接CE,作EF⊥PF
解:连接CE,作EF⊥PF∵∠DAP=∠PCE,∠APD=∠CPE,
∴△APD∽△CPE,
∴
| AP |
| CP |
| DP |
| PE |
∵P为边CD的中点
∴
| ||
| 1 |
| 1 |
| PE |
∴PE=
| ||
| 5 |
∵FE∥AD
∴△APD∽△EPF,
∴
| AP |
| PE |
| DP |
| PF |
∴
| ||||
|
| 1 |
| PF |
∴PF=
| 1 |
| 5 |
∴EF=
| 2 |
| 5 |
DE=
| DF 2+EF 2 |
2
| ||
| 5 |
△PDE的面积为
| 1 |
| 2 |
| 2 |
| 5 |
| 1 |
| 5 |
点评:此题主要考查了相似三角形的判定,以及应用和勾股定理,综合性比较强.

练习册系列答案
相关题目
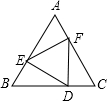 已知:如图,边长为a的正△ABC内有一边长为b的内接正△DEF,则△AEF的内切圆半径为
已知:如图,边长为a的正△ABC内有一边长为b的内接正△DEF,则△AEF的内切圆半径为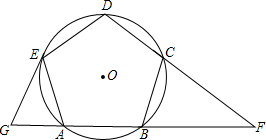
 (1997•南京)已知:如图,边长为2的等边三角形ABC,延长BC到D,使CD=BC,延长CB到E,使BE=CB,求△ADE的周长.
(1997•南京)已知:如图,边长为2的等边三角形ABC,延长BC到D,使CD=BC,延长CB到E,使BE=CB,求△ADE的周长.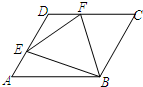 已知:如图,边长为a的菱形ABCD中,∠DAB=60°,E是异于A、D两点的动点,F是CD上的动点,请你判断:无论E、F怎样移动,当满足:AE+CF=a时,△BEF是什么三角形?并说明你的结论.
已知:如图,边长为a的菱形ABCD中,∠DAB=60°,E是异于A、D两点的动点,F是CD上的动点,请你判断:无论E、F怎样移动,当满足:AE+CF=a时,△BEF是什么三角形?并说明你的结论.