题目内容
【题目】已知关于x的二次函数y=x2+(k2﹣3k﹣4)x+2k的图象与x轴从左到右交于A,B两点,且这两点关于原点对称.
(1)求k的值;
(2)在(1)的条件下,若反比例函数y=![]() 的图象与二次函数y=x2+(k2﹣3k﹣4)x+2k的图象从左到右交于Q,R,S三点,且点Q的坐标为(﹣1,﹣1),点R(xR,yR),S(xs,ys)中的纵坐标yR,ys分别是一元二次方程y2+my﹣1=0的解,求四边形AQBS的面积S四边形AQBS;
的图象与二次函数y=x2+(k2﹣3k﹣4)x+2k的图象从左到右交于Q,R,S三点,且点Q的坐标为(﹣1,﹣1),点R(xR,yR),S(xs,ys)中的纵坐标yR,ys分别是一元二次方程y2+my﹣1=0的解,求四边形AQBS的面积S四边形AQBS;
(3)在(1),(2)的条件下,在x轴下方是否存在二次函数y=x2+(k2﹣3k﹣4)x+2k图象上的点P使得S△PAB=2S△RAB?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1)-1;(2)![]() ;(3)不存在,理由见解析
;(3)不存在,理由见解析
【解析】试题分析:(1)设A点坐标为(x1,0),B点坐标为(x2,0),由A、B两点关于原点对称,即可得x1+x2=0,又由x1+x2=﹣(k2﹣3k﹣4),即可求得k的值;
(2)由Q点的坐标求出m的值,从而确定一元二次方程y2﹣my﹣1=0即为y2+y﹣1=0,解得:y=![]() ,因为点R在点S的左边,所以yR=
,因为点R在点S的左边,所以yR=![]() ,由(1)得二次函数y=x2﹣2,令x2﹣2=0,解得:x1=-
,由(1)得二次函数y=x2﹣2,令x2﹣2=0,解得:x1=-![]() ,x2=
,x2=![]() ,所以A(﹣
,所以A(﹣![]() ,0),B(
,0),B(![]() ,0),即可求得AB的长,又由四边形AQBS的面积为:S△AQB+S△ASB求得答案;
,0),即可求得AB的长,又由四边形AQBS的面积为:S△AQB+S△ASB求得答案;
(3)由抛物线的顶点坐标为(0,﹣2),假设满足条件的点P存在,由S△PAB=2S△RAB,可得点P的纵坐标,即可得即在x轴下方抛物线上不存在点P,使S△PAB=2S△RAB.
试题解析:
(1)设A点坐标为(x1,0),B点坐标为(x2,0),
∵A、B两点关于原点对称,
∴x1+x2=0,
又x1+x2=﹣(k2﹣3k﹣4),
则k2﹣3k﹣4=0,
解得k1=﹣1,k2=4,
当k=4时,抛物线为y=x2+8,此时△=﹣32<0,舍去;
当k=﹣1时,抛物线为y=x2﹣2,此时△=8>0,则抛物线与x轴交于两点,
故所求k值为﹣1.
(2)如图:
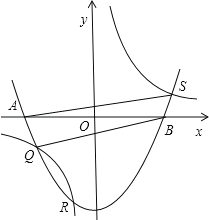
∵Q的坐标为(﹣1,﹣1),在y=![]() 上,
上,
∴-1=![]() ,
,
解得:m=1,
∴一元二次方程y2﹣my﹣1=0即为y2+y﹣1=0,
解得:y=![]() ,
,
∵点R在点S的左边,
∴yR=![]() ,
,
由(1)得二次函数y=x2﹣2,令x2﹣2=0,解得:x1=-![]() ,x2=
,x2=![]() ,
,
∴A(﹣![]() ,0),B(
,0),B(![]() ,0),
,0),
∴AB=|![]() -(-
-(-![]() )|=2
)|=2![]() ,
,
则四边形AQBS的面积为:
S△AQB+S△ASB=![]()
(3)∵抛物线的顶点坐标为(0,﹣2),假设满足条件的点P存在,
则∵S△PAB=2S△RAB,
∴点P的纵坐标为:2×(![]() )=﹣1-
)=﹣1-![]() ,
,
而﹣1﹣![]() ,
,
∴P点不存在.
即在x轴下方抛物线上不存在点P,使S△PAB=2S△RAB.

 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
