题目内容
【题目】在
中，
．
(1)如图①，以点
为直角顶点，
为腰在右侧作等腰
，过点
作
交
的延长线于点
．求证：
．
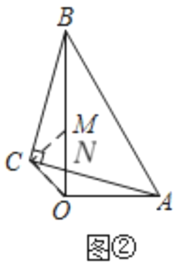
(2)如图②，以为底边在左侧作等腰，连接
，求
的度数．
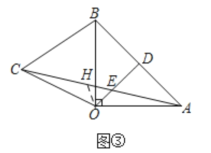
(3)如图③，中，
,垂足为点，以
为边在左侧作等边
,连接
交
于
，
,
,求的长．
【答案】（1）见解析；（2）
；（3）8
【解析】
（1）根据“一线三垂直”模型，可以证得
；
（2）过点C作CM⊥CO交BO于M，AC与BO交于点N，利用旋转模型证明
≌
，由外角的性质计算即可；
（3）在CE上截取一点H，使CH=AE，连接OH，利用等腰直角△AOB，等边△BOC证得
≌
，通过等角代换证明
为等边三角形，由线段和计算即可得到结果．
（1）∵∠BAC=∠AOB=90°，
∴∠BAO+∠DAC=∠BAO+∠ABO=90°，
∴∠DAC=∠ABO，
∵△ABC是等腰直角三角形，
∴AB=AC，
在△AOB和△CDA中，
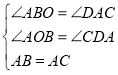
∴△AOB≌△CDA（AAS）
（2）如图②，过点C作CM⊥CO交BO于M，AC与BO交于点N，
，
，
，
，
，
∵AC=BC，
≌，
，
，
，
故答案为：135°．
（3）如图③，在CE上截取一点H，使CH=AE，连接OH，
∵△AOB是等腰直角三角形，△BOC是等边三角形，所以
，
，
≌，
，AE=CH=3，∠AOE=∠COH，
，∠AOB=90°，
，
，∠BOH=∠BOC-∠COH=60°-45°=15°，
，
为等边三角形，
，
，
故答案为：8．
练习册系列答案
中考解读考点精练系列答案
相关题目
