Question

【题目】用一条直线分割一个三角形，如果能分割出等腰三角形，那么就称这条直线为该三角形的一条等腰分割线．在直角三角形ABC中，∠C＝90°，AC＝8，BC＝6．

（1）如图（1），若 O 为 AB 的中点，则直线 OC_____△ABC 的等腰分割线（填“是”或“不是”）

（2）如图（2）已知△ABC 的一条等腰分割线 BP 交边 AC 于点 P，且 PB＝PA，请求出 CP 的长度．

（3）如图（3），在△ABC 中，点 Q 是边 AB 上的一点，如果直线 CQ 是△ABC 的等腰分割线，求线段BQ 的长度等于 ______．（直接写出答案）．

Answer 1

【答案】（1）是；（2） ；（3）5 或 2 或 6 或

【解析】

（1）根据直角三角形斜边上的中线等于斜边的一半可得结论；

（2）设 CP＝x，则 PA＝PB＝8﹣x，根据勾股定理列方程得：62+x2＝(8﹣x)2，求解即可；

（3）分情况进行讨论：

①当△ACQ 是等腰三角形时，分三种情况讨论；

②当△BCQ 是等腰三角形时，同理分三种情况讨论．

解：（1）是，如图（1），

∵∠ACB＝90°，O 为 AB 中点，

∴在Rt△ACB中，OC＝AB＝AO＝BO，

∴可得到等腰△AOC和等腰△BOC，

∴直线OC是△ABC的等腰分割线，

故答案为：是；

（2）由题可知PA＝PB，BC＝6，

设CP＝x，则PA＝PB＝8﹣x，

在Rt△BPC 中，BC2+PC2＝PB2，

∴62+x2＝（8﹣x）2，

解得：x＝，即：CP＝；

（3）BQ＝2或5或或6，

①若△ACQ 为等腰三角形，

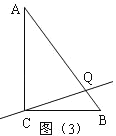
如图（3），当 AC＝AQ 时，AQ＝8，BQ＝AB﹣AQ＝2，

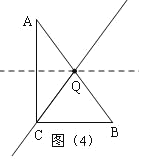
如图（4），当QC＝QA 时，Q为AB中点，BQ＝AB＝5，

当CA＝CQ 时，Q不在线段AB上，舍去；

②若△BCQ 为等腰三角形．

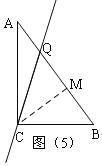
如图（5），当CQ＝CB时，过C作CM⊥AB于M，此时M为BQ的中点，

∵S△ABC＝BCAC＝ABCM，

∴×6×8＝×10CM

解得：CM＝．

在Rt△CMB中，M＝＝，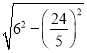

∴BQ＝2QM＝，

如图（6），当BC＝BQ时，BQ＝BC＝6．

如图（7），当QC＝QB时，Q为AB中点，BQ＝AB＝5．

综上，BQ＝2或5或或6．