Question

【题目】如图，在Rt△ABC中，∠ACB=90°，AC=BC，点M在AC边上，且AM=2，MC=6，动点P在AB边上，连接PC，PM，则PC+PM的最小值是 ．

Answer 1

【答案】2
【解析】解：如图，过点作CO⊥AB于O，延长BO到C'，使OC'=OC，连接MC'，交AB于P，

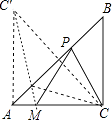
此时PC'=PM+PC'=PM+PC的值最小，

连接AC'，

∵CO⊥AB，AC=BC，∠ACB=90°，

∴∠ACO= ×90°=45°，

∵CO=OC'，CO⊥AB，

∴AC'=CA=AM+MC=8，

∴∠OC'A=∠OCA=45°，

∴∠C'AC=90°，

∴C'A⊥AC，

∴MC′= = =2 ，

∴PC+PM的最小值为2 ．

所以答案是：2 ．

【考点精析】通过灵活运用勾股定理的概念和轴对称-最短路线问题，掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；已知起点结点，求最短路径；与确定起点相反，已知终点结点，求最短路径；已知起点和终点，求两结点之间的最短路径；求图中所有最短路径即可以解答此题．