题目内容
【题目】对任意有理数x、y定义运算如下:x△y=ax+by+cxy,这里a、b、c是给定的数,等式右边是通常数的加法及乘法运算,如当a=1,b=2,c=3时,l△3=1×l+2×3+3×1×3=16,现已知所定义的新运算满足条件,1△2=3,2△3=4,并且有一个不为零的数d使得对任意有理数x△d=x,求a、b、c、d的值.
【答案】a的值为5、b的值为0、c的值为﹣1、d的值为4
【解析】
试题由x△d=x,得ax+bd+cdx=x,即(a+cd﹣1)x+bd=0,得![]() ①,由1△2=3,得a+2b+2c=3②,2△3=4,得2a+3b+6c=4③,解以上方程组成的方程组即可求得a、b、c、d的值.
①,由1△2=3,得a+2b+2c=3②,2△3=4,得2a+3b+6c=4③,解以上方程组成的方程组即可求得a、b、c、d的值.
解:∵x△d=x,∴ax+bd+cdx=x,
∴(a+cd﹣1)x+bd=0,
∵有一个不为零的数d使得对任意有理数x△d=x,
则有![]() ①,
①,
∵1△2=3,∴a+2b+2c=3②,
∵2△3=4,∴2a+3b+6c=4③,
又∵d≠0,∴b=0,
∴有方程组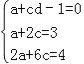
解得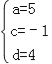 .
.
故a的值为5、b的值为0、c的值为﹣1、d的值为4.

练习册系列答案
相关题目