题目内容
若0°<α<45°,且sinαconα=3
| ||
| 16 |
分析:利用参数法,设x=sinα,y=cosβ,再根据平方关系和三角函数的增减性解答.
解答:解:设x=sinα,y=cosβ,
∵sin2α+cos2α=1,
∴x2+y2=1,
∴xy=
,
又∵0°<α<45°,
∴sinα<cosα,
则
,
将②两边平方得,x2y2=
④,
由①得,y2=1-x2⑤,
把⑤代入④得,x2(1-x2)=
,
令x2=z,
可得z2-z+
=0,
解得z1=
,z2=
.
解得x=±
或x=±
.
由于x=sinα,0°<α<45°,
故x=
或x=
,
当x=
时,y=
=
=
>
,符合③;
当x=
时,y=
=
<
,不符合③,舍去.
故答案为:
.
∵sin2α+cos2α=1,
∴x2+y2=1,
∴xy=
3
| ||
| 16 |
又∵0°<α<45°,
∴sinα<cosα,
则
|
将②两边平方得,x2y2=
| 63 |
| 256 |
由①得,y2=1-x2⑤,
把⑤代入④得,x2(1-x2)=
| 63 |
| 256 |
令x2=z,
可得z2-z+
| 63 |
| 256 |
解得z1=
| 7 |
| 16 |
| 9 |
| 16 |
解得x=±
| ||
| 4 |
| 3 |
| 4 |
由于x=sinα,0°<α<45°,
故x=
| ||
| 4 |
| 3 |
| 4 |
当x=
| ||
| 4 |
1-(
|
2
| ||
| 4 |
| ||
| 2 |
| ||
| 4 |
当x=
| 3 |
| 4 |
1-(
|
| ||
| 4 |
| 3 |
| 4 |
故答案为:
| ||
| 4 |
点评:此题考查了三角函数的增减性和三角函数的平方关系,利用参数法是解题的关键.

练习册系列答案
相关题目
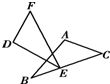 7、如图,△ABC≌△DEF,DF和AC,EF和BC是对应边.若∠A=100°,∠F=45°,则∠B等于( )
7、如图,△ABC≌△DEF,DF和AC,EF和BC是对应边.若∠A=100°,∠F=45°,则∠B等于( )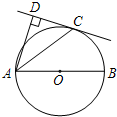 如图,C为以AB为直径的⊙O上一点,AD和过点C的切线互相垂直,垂足为点D.
如图,C为以AB为直径的⊙O上一点,AD和过点C的切线互相垂直,垂足为点D.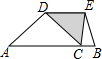 如图,一张三角形纸片△ABC,沿DE折叠使得顶点C落在边AB上,若DE∥AB,∠A=45°,则∠ADC的度数是( )
如图,一张三角形纸片△ABC,沿DE折叠使得顶点C落在边AB上,若DE∥AB,∠A=45°,则∠ADC的度数是( )