题目内容
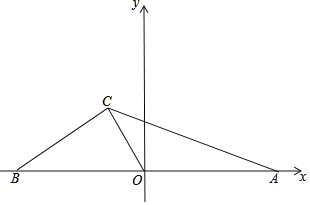
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与轴,
与轴,![]() 轴分别交于点
轴分别交于点![]() ,
,![]() .抛物线
.抛物线![]() 经过点
经过点![]() ,将点
,将点![]() 向右平移
向右平移![]() 个单位长度,得到点
个单位长度,得到点![]() .
.
(1)求点![]() 的坐标和抛物线的对称轴;
的坐标和抛物线的对称轴;
(2)若抛物线与线段![]() 恰有一个公共点,结合函数图象,求
恰有一个公共点,结合函数图象,求![]() 的取值范围.
的取值范围.
【答案】(1)C(5,4);对称轴x=1;(2)a≥![]() 或a<
或a<![]() 或a=-1.
或a=-1.
【解析】
(1)根据坐标轴上点的坐标特征可求点B的坐标,根据平移的性质可求点C的坐标;根据坐标轴上点的坐标特征可求点A的坐标,进一步求得抛物线的对称轴;
(2)结合图形,分三种情况:①a>0;②a<0,③抛物线的顶点在线段BC上;进行讨论即可求解
解:(1)与y轴交点:令x=0代入直线y=4x+4得y=4,
∴B(0,4),
∵点B向右平移5个单位长度,得到点C,
∴C(5,4);
又∵与x轴交点:令y=0代入直线y=4x+4得x=-1,
∴A(-1,0),
∵点B向右平移5个单位长度,得到点C,
将点A(-1,0)代入抛物线y=ax2+bx-3a中得0=a-b-3a,即b=-2a,
∴抛物线的对称轴x=![]() ;
;
(2)∵抛物线y=ax2+bx-3a经过点A(-1,0)且对称轴x=1,
由抛物线的对称性可知抛物线也一定过A的对称点(3,0),
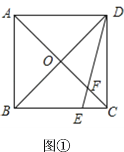
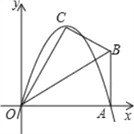
①a>0时,如图1,

将x=0代入抛物线得y=-3a,
∵抛物线与线段BC恰有一个公共点,
∴-3a<4,
a>![]() ,
,
将x=5代入抛物线得y=12a,
∴12a≥4,
a≥![]() ,
,
∴a≥![]() ;
;
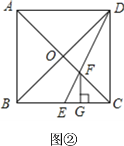
②a<0时,如图2,
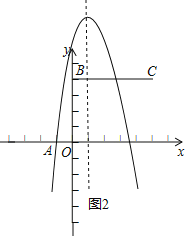
将x=0代入抛物线得y=-3a,
∵抛物线与线段BC恰有一个公共点,
∴-3a>4,
a<![]() ,
,
将x=5代入抛物线得y=12a,
∴12a<4
∴a<![]() ,
,
∴a<![]() ;
;
③当抛物线的顶点在线段BC上时,则顶点为(1,4),如图3,
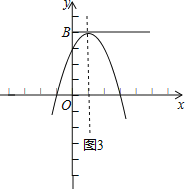
将点(1,4)代入抛物线得4=a-2a-3a,
解得a=-1.
综上所述::a≥![]() 或a<
或a<![]() 或a=-1.
或a=-1.

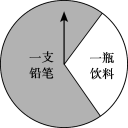
【题目】某商场有一个可以自由转动的圆形转盘(如图).规定:顾客购物100元以上可以获得一次转动转盘的机会,当转盘停止时,指针落在哪一个区域就获得相应的奖品(指针指向两个扇形的交线时,当作指向右边的扇形).下表是活动进行中的一组统计数据:
转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“铅笔”的次数m | 68 | 111 | 136 | 345 | 546 | 701 |
落在“铅笔”的频率 (结果保留小数点后两位) | 0.68 | 0.74 | 0.68 | 0.69 | 0.68 | 0.70 |
(1)转动该转盘一次,获得铅笔的概率约为_______;(结果保留小数点后一位)
(2)铅笔每只0.5元,饮料每瓶3元,经统计该商场每天约有4000名顾客参加抽奖活动,请计算该商场每天需要支出的奖品费用;
(3)在(2)的条件下,该商场想把每天支出的奖品费用控制在3000元左右,则转盘上“一瓶饮料”区域的圆心角应调整为______度.