题目内容
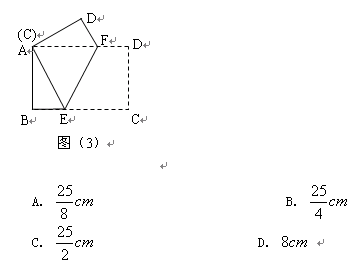
如图,四边形ABCD中,AD∥BC,AF=CE,BE⊥AC于E,DF⊥AC于F.
试判断DC与AB的位置关系,并说明理由.
试判断DC与AB的位置关系,并说明理由.

DC∥AB, 理由见解析
解:DC∥AB,理由如下:
∵AD∥BC
∴∠DAF=∠BCE
又∵BE⊥AC,DF⊥AC
∴∠DFA=∠BEC=90°
又∵AF=CE
∴△DFA≌△BEC
∴AD=BC,而 AD∥BC
∴四边形ABCD是平行四边形
∴DC∥AB
证得△DFA≌△BEC,得出AD=BC,又已知AD∥BC,从而得出结论
∵AD∥BC
∴∠DAF=∠BCE
又∵BE⊥AC,DF⊥AC
∴∠DFA=∠BEC=90°
又∵AF=CE
∴△DFA≌△BEC
∴AD=BC,而 AD∥BC
∴四边形ABCD是平行四边形
∴DC∥AB
证得△DFA≌△BEC,得出AD=BC,又已知AD∥BC,从而得出结论

练习册系列答案
相关题目
 ,则∠A= 度.
,则∠A= 度.


 0分积的和是32cm²,四边形ABCD的面积是20cm²。问甲、乙、丙、丁四个长方形周长的总和是:
0分积的和是32cm²,四边形ABCD的面积是20cm²。问甲、乙、丙、丁四个长方形周长的总和是:
 、
、 是等腰梯形
是等腰梯形 的两条对角线.证明:
的两条对角线.证明:
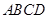 中,
中, ,
, ,现将其沿
,现将其沿 对折,使得点
对折,使得点 与点
与点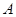 重合,则
重合,则 长为( )
长为( )