��Ŀ����
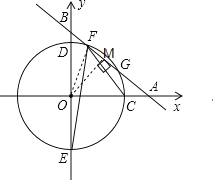
����Ŀ����ͼ��ƽ��ֱ������ϵxOy�У�һ�κ���y=��![]() x+b��bΪ������b��0����ͼ����x�ᡢy��ֱ��ཻ�ڵ�A��B���뾶Ϊ4�ġ�O��x���������ཻ�ڵ�C����y���ཻ�ڵ�D��E����D�ڵ�E�Ϸ���
x+b��bΪ������b��0����ͼ����x�ᡢy��ֱ��ཻ�ڵ�A��B���뾶Ϊ4�ġ�O��x���������ཻ�ڵ�C����y���ཻ�ڵ�D��E����D�ڵ�E�Ϸ���

��1����ֱ��AB��![]() ����������F��G��
����������F��G��
�����CFE�Ķ�����
���ú�b�Ĵ���ʽ��ʾFG2����ֱ��д��b��ȡֵ��Χ��
��2����b��5�����߶�AB���Ƿ���ڵ�P��ʹ��CPE=45�㣿�����ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��45������2��4��b��5����3������ P��![]() ��
�� ![]() ����
����
�������������������1���١�EOC�͡�EFC��![]() ���Ե�Բ�ĽǺ�Բ�ܽǣ�����ͬ�����Ե�Բ�ܽ���Բ�Ľǵ�һ�������⼴�ɣ�
���Ե�Բ�ĽǺ�Բ�ܽǣ�����ͬ�����Ե�Բ�ܽ���Բ�Ľǵ�һ�������⼴�ɣ�
�ڹ�O��OM��FG�ڵ�M������OF�������һ�κ���ͼ����x�ᡢy�ύ��A��B�����꣬Ȼ����ݹ��ɶ������AB�ij�������������������OM�ij��������ù��ɶ�����ʾ��FM2�����ɴ���������FG��2FM���������Ա�ʾ��FG2���ٸ���ʽ��д��b�ķ�Χ��
��2������ǰ�����OM��![]() ����b��5ʱ��ֱ����Բ���룬��b��5ʱ��ֱ����Բ���У�����OP��������ֱ�ߴ�ֱʱ����ϵ���Ļ�Ϊ��1���OP�Ľ���ʽ��Ȼ��������������ʽ���������P�����꣮
����b��5ʱ��ֱ����Բ���룬��b��5ʱ��ֱ����Բ���У�����OP��������ֱ�ߴ�ֱʱ����ϵ���Ļ�Ϊ��1���OP�Ľ���ʽ��Ȼ��������������ʽ���������P�����꣮
���������
�⣺��1���١ߡ�COE��90����
���CFE��![]() ��COE��45����
��COE��45����
����ͼ����OM��AB��M������OF��
��ֱ�ߵĺ���ʽΪ��y��![]() ��
��
��B��������0��b����A��������![]() ��0����
��0����
��AB��![]()
��![]() ��
��
��Rt��OBC�У���������ɵ�
OA��OB��AB��OM��
�ã�OM��![]() ��
��
��OF��4��
��FM2��OF2��OM2��42����![]() ��2 ��
��2 ��
��OM��FG��
��FG��2FM��
��FG2��4FM2��4��[42����![]() ��2 ]��64��
��2 ]��64��![]() b2��
b2��
��ֱ��AB��![]() ����������F��G��
����������F��G��
��4��b��5��
��2�����ڣ�
��ͼ��
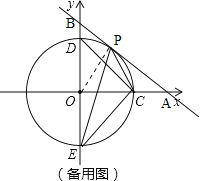
��b��5ʱ��OM��![]() ��4����ֱ����Բ���룬��CPE��45�㣻
��4����ֱ����Բ���룬��CPE��45�㣻
��b��5ʱ��OM��![]() ��4����ֱ����Բ���У�
��4����ֱ����Բ���У�
��DE��ֱ����
���DCE��90����
��CO��DE����DO��EO��
���ODC����OEC��45����
���CPE����ODC��45����
����ڵ�P��ʹ��CPE��45�㣬
����OP��
��P���е㣬��OP��AB����OP���ڵ�ֱ��Ϊ��y��![]() ��
��
�֡�AB���ڵ�ֱ��Ϊ��y��![]() ��5��
��5��
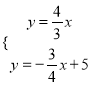
���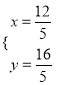
��P��![]() ��
�� ![]() ����
����



