题目内容
【题目】“牟合方盖”是由我国古代数学家刘徽首先发现并采用的一种用于计算球体体积的方法，“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体，如图所示的几何体是可以形成“牟合方盖”的一种模型，它的主视图、左视图、俯视图依次是（ ）
A.（2）、（4）、（1）B.（3）、（1）、（2）
C.（1）、（4）、（2）D.（3）、（4）、（1）
【答案】D
【解析】
利用组合体的形状，结合三视图的定义即可得出正确选项．
该几何体的主视图有两层，底层是两个正方形，上层的右边是一个正方形；左视图是一列两个正方形，底层的正方形里面有一个圆；俯视图是一行两个正方形，右边的正方形里面有一个圆．
∴它的主视图、左视图、俯视图依次是（3）（4）（1）．
故选：D．
练习册系列答案
名校课堂系列答案
相关题目
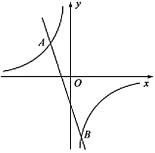
【题目】如图，一次函数y＝x＋m的图象与反比例函数y＝
的图象交于A，B两点，且与x轴交于点C，点A的坐标为(2，1)．
(1)求m及k的值；
(2)求点C的坐标，并结合图象写出不等式组0＜x＋m≤
的解集．
【题目】2020年，新型冠状病毒肆虐全球，疫情期间学生在家进行网课学习和锻炼，学习和身体健康状况都有一定的影响．为了解学生身体健康状况，某校对学生进行立定跳远水平测试．随机抽取50名学生进行测试，并把测试成绩（单位：m）绘制成不完整的频数分布表和频数分布直方图．
学生立定跳远测试成绩的频数分布表
分组 | 频数 |
| a |
| 12 |
| b |
| 10 |
学生立定跳远测试成绩的频数分布直方图
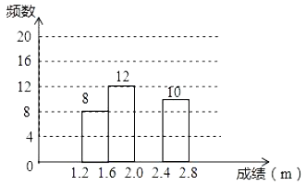
请根据图表中所提供的信息，完成下列问题：
（1）表中
________，
________；
（2）样本成绩的中位数落在________范围内；
（3）请把频数分布直方图补充完整；
（4）该校共有1200名学生，估计该学校学生立定跳远成绩在
范围内的有多少人？
