Question

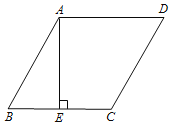
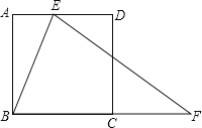
【题目】如图，E是正方形ABCD的边AD上的动点，F是边BC延长线上的一点，且BF=EF，AB=12，设AE=x，BF=y．

（1）当△BEF是等边三角形时，求BF的长；

（2）求y与x的函数解析式，并写出它的定义域；

（3）把△ABE沿着直线BE翻折，点A落在点A′处，试探索：△A′BF能否为等腰三角形？如果能，请求出AE的长；如果不能，请说明理由．

Answer 1

【答案】（1）；（2）（0＜x＜12）；（3）能，

【解析】

（1）当△BEF是等边三角形时，求得∠ABE=30°，则可解Rt△ABE，求得BF即BE的长．

（2）作EG⊥BF，垂足为点G，则四边形AEGB是矩形，在Rt△EGF中，由勾股定理知，EF2=（BF-BG）2+EG2．即y2=（y-x）2+122．故可求得y与x的关系．

（3）当把△ABE沿着直线BE翻折，点A落在点A'处，应有∠BA'F=∠BA'E=∠A=90°，若△A'BF成为等腰三角形，必须使A'B=A'F=AB=12，有FA′=EF-A′E=y-x=12，继而结合（2）得到的y与x的关系式建立方程即可求得AE的值．

（1）当△BEF是等边三角形时，∠EBF=90°，

∵四边形ABCD是正方形，

∴∠ABC=∠A=90°，

∴∠ABE=∠ABC-∠EBC=90°-60°=30°，

∴BE=2AE，

设AE=x，则BE=2x，

在Rt△ABE中，AB2+AE2=BE2，

即122+x2=(2x)2，解得x=

∴AE=，BE=，

∴BF=BE=．

（2）作EG⊥BF，垂足为点G，

根据题意，得EG=AB=12，FG=y-x，EF=y，0＜AE＜12，

在Rt△EGF中，由勾股定理知，EF2=（BF-BG）2+EG2．

∴y2=（y-x）2+122，

∴所求的函数解析式为（0＜x＜12）．

（3）∵AD∥BC

∴∠AEB=∠FBE

∵折叠

∴∠AEB=∠FEB，

∴∠AEB=∠FBE=∠FEB，

∴点A′落在EF上，

∴A'E=AE，∠BA'F=∠BA'E=∠A=90，

∴要使△A'BF成为等腰三角形，必须使A'B=A'F．

而A'B=AB=12，A'F=EF-A'E=BF-A'E，

∴y-x=12．

∴-x=12．

整理得x2+24x-144=0，

解得，

经检验：都原方程的根，

但不符合题意，舍去，

当AE=时，△A'BF为等腰三角形．