Question

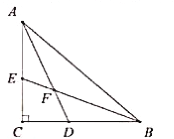
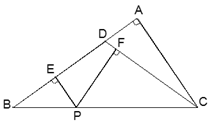
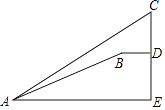
【题目】如图，ΔABC中，CD是AB边上的高，AC=8，∠ACD=30°，tan∠ACB= ,点P为CD上一动点，当BP+CP最小时，DP=_________.

Answer 1

【答案】

【解析】作 PE⊥AC 于 E，BE′⊥AC 于 E′ 交 CD 于 P′.

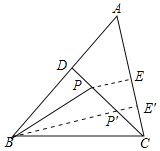
∵CD⊥AB，∠ACD=30°，∠PEC=90°，AC=8 ，

∴PE=PC，∠A=60°，∠ABE′=30°，AD=4，CD=4，

∴PB+PC=PB+PE ，

∴ 当 BE′⊥AC 时 ，PB+PE=BP′+P′E′=BE′最小，

∵tan∠ACB==，设 BE′=5k，CE′=3k ，

∴AE′=83k，AB=166k，BD=166k4=126k ，

∴BC2=BD2+CD2=BE′2+CE′2 ，

∴(126k)2+48=9k2+75k2 ，

整理得 k2+3k4=0 ，

∴k=1或4( 舍去 ) ，

∴BE′=5，CE′=3

在Rt△CE′P′中，∠ACD=30°，CE′=3，可求得CP′=2，

∴DP′=CD-CP′=4-2=2.