Question

【题目】已知A(0，1)，B(2，0)，C(4，3)．

(1)在坐标系中描出各点，画出三角形ABC；

(2)求三角形ABC的面积；

(3)设点P在坐标轴上，且三角形ABP与三角形ABC的面积相等，请直接写出点P的坐标．

Answer 1

【答案】(1) 见解析；（2）4；（3）点P的坐标为(10，0)或(－6，0)或(0，5)或(0，－3)

【解析】分析：(1)、在平面直角坐标系中描出各点，从而得出三角形；(2)、利用矩形的面积减去三个直角三角形的面积得出△ABC的面积；(3)、根据三角形的面积得出三角形的底，从而得出点的坐标．

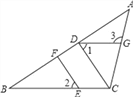
详解：(1)三角形ABC如图所示

如图，过点C向x轴、y轴作垂线，垂足为D，E.

∴S长方形DOEC＝3×4＝12，S三角形BCD＝×2×3＝3，

S三角形ACE＝×2×4＝4，S三角形AOB＝×2×1＝1，

∴S三角形ABC＝S长方形DOEC－S三角形ACE－S三角形BCD－S三角形AOB＝12－4－3－1＝4 ，

(3)点P的坐标为(10，0)或(－6，0)或(0，5)或(0，－3)