题目内容
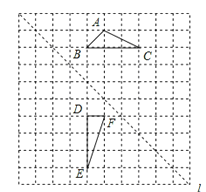
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC和△DEF(顶点为网格线的交点),以及过格点的直线l.
①将△ABC向右平移两个单位长度,再向下平移两个单位长度,画出平移后的三角形△A’B’C’;
②画出△DEF关于直线l对称的三角形△D’E’F’;
③填空:∠C+∠E= .
【答案】①见解析;②见解析;③45°.
【解析】分析:(1)、将点A、B、C分别右移2个单位、下移2个单位得到其对应点,顺次连接即可得;(2)、分别作出点D、E、F关于直线l的对称点,顺次连接即可得;(3)、连接A′F′,利用勾股定理逆定理证△A′C′F′为等腰直角三角形即可得.
详解:(1)△A′B′C′即为所求;
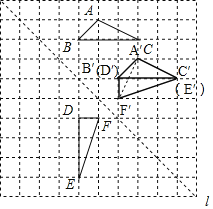
(2)△D′E′F′即为所求;
(3)如图,连接A′F′, ∵△ABC≌△A′B′C′、△DEF≌△D′E′F′,
∴∠C+∠E=∠A′C′B′+∠D′E′F′=∠A′C′F′,
∵A′C′=![]() ,A′F′=
,A′F′=![]() ,C′F′=
,C′F′=![]() ,
,
∴A′C′2+A′F′2=5+5=10=C′F′2, ∴△A′C′F′为等腰直角三角形,
∴∠C+∠E=∠A′C′F′=45°,

练习册系列答案
相关题目