题目内容
【题目】如图,已知A、B、C分别是⊙O上的点,∠B=60°,P是直径CD的延长线上的一点,且AP=AC.
(1)求证:AP与⊙O相切;
(2)如果PD=![]() ,求AP的长.
,求AP的长.

【答案】(1)证明参见解析;(2)3.
【解析】
试题分析:(1)利用圆周角定理以及等腰三角形的性质,得出∠P=∠ACP=∠OCA=∠OAC=30°,∠PAC=120°,进而得出∠PAO=90°,即可得出答案;(2)首先根据直角三角形中30°角所对的直角边等于斜边的一半求得半径,从而求得OA、OP,进而利用勾股定理得出AP的长.
试题解析:(1)如图:连接AO,
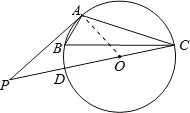 ∵∠B=60°,∴∠AOC=120°,∵AO=CO,AP=AC,∴∠P=∠ACP,∠OCA=∠OAC=30°,∴∠P=∠ACP=∠OCA=∠OAC=30°,∴∠PAC=120°,∴∠PAO=90°,∴AP是⊙O的切线;(2)设⊙O的半径为R,则OA=OD=R,PD=
∵∠B=60°,∴∠AOC=120°,∵AO=CO,AP=AC,∴∠P=∠ACP,∠OCA=∠OAC=30°,∴∠P=∠ACP=∠OCA=∠OAC=30°,∴∠PAC=120°,∴∠PAO=90°,∴AP是⊙O的切线;(2)设⊙O的半径为R,则OA=OD=R,PD=![]() ,∴OP=
,∴OP=![]() +R,∵∠PAO=90°,∠P=30°,∴OP=2OA,即
+R,∵∠PAO=90°,∠P=30°,∴OP=2OA,即![]() +R=2R,解得R=
+R=2R,解得R=![]() ,∴OA=
,∴OA=![]() ,OP=2
,OP=2![]() ,根据勾股定理得:PA=
,根据勾股定理得:PA=![]() ,AP=
,AP=![]() =
=![]() =3.故AP长为3.
=3.故AP长为3.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目