题目内容
【题目】已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M,N.
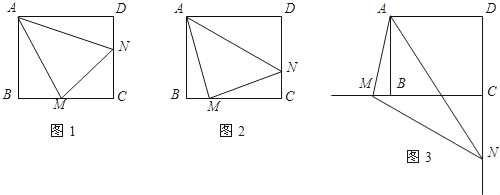
(1)当∠MAN绕点A旋转到如图1的位置时,求证:BM+DN=MN;
(2)当∠MAN绕点A旋转到BM≠DN时(如图2),则线段BM,DN和MN之间数量关系是 ;
(3)当∠MAN绕点A旋转到如图3的位置时,猜想线段BM,DN和MN之间又有怎样的数量关系呢?并对你的猜想加以说明.
【答案】(1)详见解析;(2)BM+DN=MN;(3)DN﹣BM=MN,理由详见解析.
【解析】
(1)延长CB至E使得BE=DN,连接AE,连接AC,证明△ABE≌△AND和△EAM≌△NAM,得到MN=ME,即可证明BM+DN=MN;
(2)延长CB至E,使得BE=DN,连接AE,证明△ABE≌△AND和△EAM≌△NAM,MN=ME,即可证明BM+DN=MN;
(3)在DC上截取DE=BM,连接AE,可前面知△ABM≌△ADE,进一步可证明△MAN≌△EAN,可得到MN=NE,从而可得到DN-BM=MN.
(1)证明:如图1,延长CB至E使得BE=DN,连接AE,
∵四边形ABCD是正方形,
∴AB=AD,∠D=∠ABC=90°=∠ABE,
在△ADN和△ABE中
∵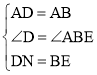 ,
,
△ABE≌△ADN(SAS),
∴∠BAE=∠DAN,AE=AN,
∴∠EAN=∠BAE+∠BAN=∠DAN+∠BAN=90°,
∵∠MAN=45°,
∴∠EAM=∠MAN,
∵在△EAM和△NAM中
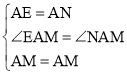 ,
,
∴△EAM≌△NAM,
∴MN=ME,
∵ME=BM+BE=BM+DN,
∴BM+DN=MN;
(2)解:线段BM,DN和MN之间数量关系是BM+DN=MN,理由如下:
延长CB至E,使得BE=DN,连接AE,
∵四边形ABCD是正方形,
∴AB=AD,∠D=∠ABC=90°=∠ABE,
在△ADN和△ABE中,
∵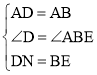 ,
,
∴△ABE≌△ADN(SAS),
∴∠BAE=∠DAN,AE=AN,
∴∠EAN=∠BAE+∠BAN=∠DAN+∠BAN=90°,
∵∠MAN=45°,
∴∠EAM=∠MAN,
∵在△EAM和△NAM中
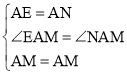 ,
,
∴△EAM≌△NAM,
∴MN=ME,
∵ME=BM+BE=BM+DN,
∴BM+DN=MN,
故答案为:BM+DN=MN;
(3)DN﹣BM=MN,理由如下:
如图3,在DC上截取DE=BM,连接AE,
由(1)知△ADE≌△ABM(SAS),
∴∠DAE=∠BAM,AE=AM,
∴∠EAM=∠BAM+∠BAE=∠DAE+∠BAE=90°,
∵∠MAN=45°,
∴∠EAN=∠MAN.
∵在△MAN和△EAN中,
 ,
,
∴△MAN≌△EAN(SAS),
∴EN=MN,
即DN﹣DE=MN,
∴DN﹣BM=MN.


 阅读快车系列答案
阅读快车系列答案【题目】在元旦期间,某商场计划购进甲、乙两种商品.
(1)已知甲、乙两种商品的进价分别为30元,70元,该商场购进甲、乙两种商品共50件需要2300元,则该商场购进甲、乙两种商品各多少件?
(2)该商场共投入9500元资金购进这两种商品若干件,这两种商品的进价和售价如表所示:
甲 | 乙 | |
进价(元/件) | 30 | 70 |
售价(元/件) | 50 | 100 |
若全部销售完后可获利5000元(利润=(售价﹣进价)×销量),则该商场购进甲、乙两种商品各多少件?
【题目】截至2019年5月,山西省政府大力实施的建设“山西农谷”战略成果初现,“山西农谷”通过组建山西农谷生物科技研究院,逐步建成大学生“互联网+农业”创新创业园.某校科技小组到该创业园的全环境智能番茄特色小镇进行综合实践活动,随机调查了60株“农谷一号“番茄的挂果数量(单位:个),并绘制了如下不完靠的统计图表:
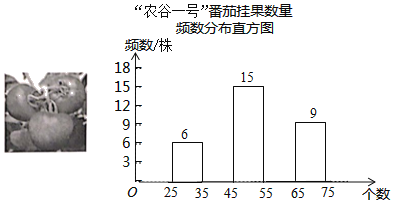
“农谷一号”番茄挂果数量统计表
挂果数量x(个) | 频数(株) | 频率 |
25≤<35 | 6 | |
35≤x<45 | 0.2 | |
45≤x<55 | 15 | a |
55≤x<65 | ||
65≤x<75 | 9 |
请结合图表中的信息解答下列问题:
(l)统计表中,a= ,若绘制“农谷一号”番茄挂果数量扇形统计图,则挂果数量在“35≤x<45”所对应扇形的圆心角度数为 ;
(2)将频数分布直方图补充完整;
(3)若所种植的“农谷一号”番茄有1000株,请估计挂果数量在“55≤x<65”范围的番茄株数.