��Ŀ����
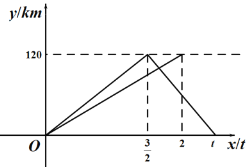
����Ŀ��һ���γ��Ӽ�ʻ���ҵأ������ҵغ��������ؼأ��ٶ���ԭ����1.5������������tСʱ.һ������ͬʱ�Ӽ�ʻ���ҵأ������ҵغ�ֹͣ.����ͬʱ������������ʻ����γ���ʻ��ʱ��Ϊx��h���������뿪�صľ���Ϊy��km����������ʻ������y��x֮��ĺ���ͼ����ͼ��ʾ.
��1���γ����ҵط��ؼص��ٶ�Ϊ km/t��t= h��
��2����γ����ҵط��ؼ�ʱy��x֮��ĺ�����ϵʽ��
��3�����γ��Ӽط����ҵص�;�����������ʱ�������������صľ���.
���𰸡�(1) 120��![]() ;(2) y=-120x+300; (3) 100km.
;(2) y=-120x+300; (3) 100km.
����������1������ͼ��ɵõ�x=![]() Сʱʱ����صľ�����120ǧ�ף�������ýγ��Ӽص��ҵص��ٶȣ�������ýγ����ҵط��ؼص��ٶȺ�t��ֵ��
Сʱʱ����صľ�����120ǧ�ף�������ýγ��Ӽص��ҵص��ٶȣ�������ýγ����ҵط��ؼص��ٶȺ�t��ֵ��
��2�����ô���ϵ����������⣻
��3�����ô���ϵ������ýγ����ҵص��صĺ�������ʽ�ͻ���·�̺�ʱ��ĺ�������ʽ�������꼴�ɣ�
��1��120��![]() .
.
��2����γ����ҵط��ؼصĺ�����ϵʽΪ��y=kx+b.
����![]() ��120���ͣ�
��120���ͣ�![]() ��0��������������룬��
��0��������������룬��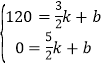 ��
��
��ã�![]() ��
��
���Խγ����ҵط��ؼ�ʱy��x֮��ĺ�����ϵʽΪ��y=-120x+300;
��3��������Ӽ�ʻ���ҵصĺ�����ϵʽΪ��y=ax ���㣨2,120�������ã����a=60���ʻ����Ӽ�ʻ���ҵ�ʱy��x֮��ĺ�����ϵʽΪ��y=60x.
��ͼ���֪���γ����ҵط��ؼ�ʱ������������·����ȣ���-120x+300=60x ���x=![]() ,��x=
,��x=![]() ʱ��y=100. �����������صľ���Ϊ100km
ʱ��y=100. �����������صľ���Ϊ100km

����Ŀ��ij��ˮ��������������A�е�һ��ˮ�������������ۣ��л������������䷽ʽ����������е���ľ�Ϊ200Ԫ/ʱ��������Ҫ�ο��������£�
���乤�� | ;��ƽ���ٶ� (ǧ��/ʱ) | �˷� (Ԫ/ǧ��) | װж���� (Ԫ) |
�� | 100 | 15 | 2000 |
���� | 80 | 20 | 900 |
(1)���ѡ���������ܷ��ñ�ѡ����ܷ��ö�1100Ԫ����ô��֪��������A��֮���·���Ƕ���ǧ���������з��̽��
(2)��A����ij��֮���·��Ϊsǧ�ף���֪������������·�ϵ����ʱ��ֱ�Ϊ2Сʱ��3.1Сʱ��Ҫ�뽫����ˮ���������н������ۣ���sΪ����ʱ��ѡ��������������������ͬ��