Question

【题目】如图，直线y＝－x＋4与x轴、y轴分别交于A、B两点，直线BC与x轴、y轴分别交于C、B两点，连接BC，且 ．

（1）求点A的坐标及直线BC的函数关系式；
（2）点M在x轴上，连接MB，当∠MBA+∠CBO=45°时，求点M的坐标；
（3）若点P在x轴上，平面内是否存在点Q，使点B、C、P、Q为顶点的四边形是菱形？若存在，请直接写出点Q的坐标；若不存在，请说明理由．

Answer 1

【答案】
（1）解；对于直线y=x+4，令x=0的y=4，令y=0得x=4，

∴A(4,0),B(0,4)，

∴OB=OA=4，

∵OC= OB，

∴OC=3，

∴C(3,0)，

设直线BC的解析式为y=kx+b,则有 ，

解得 ，

∴直线BC的解析式为y= x+4.

（2）解：如图1中，

当点M在点A的左边时，

∵OB=OA=4,∠AOB=90°，

∴∠ABO=45°，

∴∠CBO+∠MBA=∠MBA+∠MBO=45°，

∴∠CBO=∠OBM，

∵∠CBO+∠BCO=90°,∠BMO+∠OBM=90°，

∴∠BCO=∠BMO，

∴BC=BM，OC=OM=3，

∴M(3,0)，

作点M关于直线AB的对称点N,作直线BN交x轴于M ,则∠M BA=∠MBA,点M 满足条件.

∵N(4,1),B(0,4)，

∴直线BN的解析式为y= x+4,令y=0,得x= ，

∴M ( ,0)，

综上所述,满足条件的点点M的坐标为(3,0)或( ,0)

（3）解：如图2中，

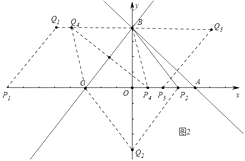
∵BC= =5，

当BC为菱形的边时,四边形CPQB,四边形CPQB,四边形BCQP是菱形,此时Q (5,4),Q (5,4),Q (0,4)，

当BC是菱形的对角线时,四边形 是菱形,可得 (256,4).

综上所述,满足条件的点Q的坐标为(5,4)或(5,4)或(0,4)或( ,4).

【解析】（1）分别令y、x等于0，求出直线与x、y轴的交点坐标，由线段OC转化为坐标；（2）分类讨论：点M在点A的左边或在A的右侧，对45度角进行转化，可求出BC关于y轴对称或BM关于y=-x+4的对称直线；（3）可分类讨论，就定线段BC为边，或为对角线，进行分类.