题目内容
【题目】如图，平面直角坐标系中，将含30°的三角尺的直角顶点C落在第二象限．其斜边两端点A、B分别落在x轴、y轴上，且AB=12cm
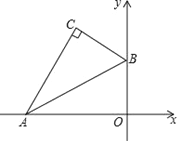
（1）若OB=6cm．①求点C的坐标；②若点A向右滑动的距离与点B向上滑动的距离相等，求滑动的距离；
（2）点C与点O的距离的最大值= cm．
【答案】（1）①C（
，9）；②
；（2）12．
【解析】试题分析：（1）①过点C作y轴的垂线，垂足为D，利用含30°角的直角三角形的性质解答即可；
②设点A向右滑动的距离为x，则点B向上滑动的距离也为x，利用三角函数和勾股定理进行解答即可；
（2）过C作CE⊥x轴，CD⊥y轴，垂足分别为E，D，得到△ACE∽△BCD，再利用相似三角形的性质解答．
试题解析：（1）①过点C作y轴的垂线，垂足为D，如图1：
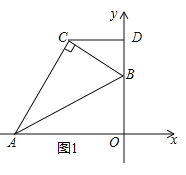
在Rt△AOB中，AB=12，OB=6，则BC=6，∴∠BAO=30°，∠ABO=60°，又∵∠CBA=60°，∴∠CBD=60°，∠BCD=30°，∴BD=3，CD=
，所以点C的坐标为（
，9）；
②设点A向右滑动的距离为x，根据题意得点B向上滑动的距离也为x，如图2：
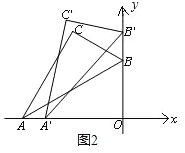
AO=12×cos∠BAO=12×cos30°=
，∴A'O= 
，B'O=6+x，A'B'=AB=12，在△A'O B'中，由勾股定理得， 
，解得：x=
，∴滑动的距离为
；
（2）设点C的坐标为（x，y），过C作CE⊥x轴，CD⊥y轴，垂足分别为E，D，如图3：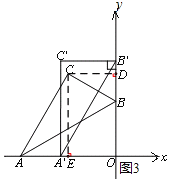
则OE=﹣x，OD=y，∵∠ACE+∠BCE=90°，∠DCB+∠BCE=90°，∴∠ACE=∠DCB，又∵∠AEC=∠BDC=90°，∴△ACE∽△BCD，∴
，即
，∴
， 
=
=
，∴当
取最大值时，即C到y轴距离最大时， 
有最大值，即OC取最大值，如图，即当C'B'旋转到与y轴垂直时，此时OC=12，故答案为：12．
